Deşifre metni
1 FEDERAL EĞİTİM AJANSI DEVLET YÜKSEK MESLEKİ EĞİTİM KURUMU “Akademisyen SP KOROLEVA'nın adını taşıyan SAMARA DEVLET HAVACILIK UZAY ÜNİVERSİTESİ” ÇOKLU ENTEGRAL görevler ve alıştırmalar Üniversitenin Yayın ve Yayın Kurulu tarafından metodolojik talimatlar olarak onaylandı S A M A R A Yayınevi SSAU
2 UDC 7 7 OM Karpilova Hakem Teknik Bilimler Adayı Doçent GN Gutman tarafından derlenmiştir Çoklu integral problemleri ve alıştırmaları: gösterge / kompozisyon yöntemi OM Karpilova Samara: Samara Devlet Havacılık ve Uzay Üniversitesi Yayınevi Koleksiyon, konulara göre tipik problemlerin çözüm örneklerini içerir: çift katlı integraller üç katlı integraller çoklu integrallerin uygulamaları Her konuda tipik problemler tartışılır, bunları çözme yöntemleri ayrıntılı olarak analiz edilir ve bağımsız çalışma için problemler önerilir. Ek, bireysel ödevler için seçenekler sunar. Tüm ödevler programa uygun olarak derlenmiştir. teknik üniversite öğrencilerine yönelik matematik dersi için Genel Mühendislik Eğitimi Bölümünde hazırlanan ve Samara Devlet Havacılık ve Uzay Üniversitesi Enerji ve Ulaştırma Enstitüsü öğrencilerine yönelik metodolojik talimatlar UDC 7 7 Samara Devlet Havacılık ve Uzay Üniversitesi.
3 KARTEZYEN KOORDİNATLARDA ÇİFT İNTEGRALLERİN HESAPLANMASI Bir çift katlı integrali hesaplamak için, tekrarlanan bir çift katlı integral f f şeklinde sunulur Örneklerin çözümü Örnek b a f'den tekrarlı bir integrale gidin ve alan aşağıdakilerle sınırlıysa integralin sınırlarını belirleyin: çizgiler: a 6; B; V; ABC üçgeninin d konturu burada A; B;6C;; d Çözüm: a Bir bölge oluşturun: O eksenine paralel bir düz çizgi; O eksenine paralel düz çizgi; 6 ve 6 numaralı noktalardan geçen 6 çizgi; Alan ABC üçgenidir Şekil C noktasının koordinatlarını bulmak için denklem sistemini çözmeniz gerekir Şekil 6 Dolayısıyla C; Dolayısıyla bölgenin içinde nasıl değiştiğini bulmak için O eksenine paralel ve bölgeyi kesen bir düz çizgi çiziyoruz. Bu düz çizgi bölgeye a doğrusu boyunca giriyor ve 6 veya 6 çizgisi boyunca çıkıyor. Dolayısıyla 6 bölgesi. bir eşitsizlik sistemi ile tanımlanabilir: 6 Artık çift katlı integralde limitleri belirlemek kolaydır: f 6 f
4 b Hadi oluşturalım: O eksenine paralel düz bir parabol Şekil. A ve B noktalarının koordinatlarını bulun Bunu yapmak için sistemi çözün ± O eksenine paralel ve bölgeyi kesen düz bir çizgi çizin Bu doğru bölgeye girer. bir parabol ve düz bir çizgi boyunca yaprakları Şekil Böylece, bölge f f eşitsizlikleri ile tanımlanır: Bu nedenle, alanı oluşturalım Şekil: köşesi orijinde olan, O eksenine göre simetrik bir parabol; köşe noktası koordinatların orijininde olan bir parabolün O eksenine göre simetrik pozitif dalı Şekil. Bu doğruların kesişme noktalarını bulalım: Denklemin her iki tarafının karesini alarak buradan elde ettiğimiz denklem Böylece doğrular kesişir O noktalarında; ve A; O'ya paralel ve alanı kesen düz bir çizgi çizdikten sonra giriş çizgisi ve çıkış çizgisinin olduğunu görüyoruz.
5 Böylece: öyleyse f f g bir üçgen oluşturalım fig Çizimden, alanın içinde O'ya paralel ve alanı kesen bir düz çizginin üçgene AC kenarı boyunca girdiği ve AB kenarı boyunca çıktığı açıktır. iki M ve M noktası şu şekildedir: Bu formülü kullanarak AB ve AC kenarlarının denklemlerini yazacağız: AB: nereden geliyorlar; 6 AC: bunlar nereden geliyor Böylece: Bu nedenle f f d Bir bölge oluşturalım Bunu yapmak için sınır denklemini dönüştürüyoruz: Değişkene göre tam bir kare seçelim: Ortaya çıkan denklem, yarıçapı merkezi olan bir daireyi tanımlıyor. bir nokta; Şekil Şekil Şekil İntegral sınırlarını belirlemek için bölgeye giriş ve bölgeden çıkış çizgisinin dairesinin üst ve alt yarısının denklemlerini yazmanız gerekir. Orijinal denklemi aşağıdakine göre çözelim: ±
6 Çemberin üst yarısının alttakinin denklemine karşılık geldiği açıktır. Dolayısıyla: bu nedenle f f Örnek İntegral sırasını değiştirin: b 6 ; ff; a c f f Çözüm: a İntegrasyon bölgesi eşitsizlik sistemi tarafından verilmektedir: Bölgeyi oluşturalım Şekil 6: parabolün üst yarısı parabolün alt yarısı İntegral sırası değiştirildiğinde integral c f Şekil 6 formunu alacaktır. 6 Parabol ile doğrunun kesişme noktalarının koordinatlarını bulun: ± Böylece A; İÇİNDE; Alanı kesen O eksenine paralel bir doğru çizelim. Bunun alana giriş çizgisi bir paraboldür; dolayısıyla alan bir eşitsizlik sistemiyle de tanımlanabilir: O halde f f 6.
7 b Bu durumda integrasyon bölgesi bir eşitsizlik sistemi tarafından verilmektedir: 6 Şekil 7'de bu bölgeyi oluşturalım: 6 hiperbol düz çizgisi A ve B noktalarının koordinatlarını bulalım A noktasında dolayısıyla B noktasında dolayısıyla Böylece A; İÇİNDE; İntegral sırasını değiştirdiğinizde integral f şeklini alacaktır Şekil 7 c O zamandan beri c ; O eksenine paralel ve bölgeyi kesen bir doğru çizelim. Giriş çizgisi 6 buradan itibaren bir hiperboldür. Çıkış çizgisi ise 6 eşitsizliği ile tanımlanır: 6 Son olarak 6 6 f f'yi elde ederiz. Alanları oluşturalım: ve: Alanın sınırı aşağıdaki denklemle belirlenir ± Denklemin her iki tarafının karesi alınarak parabolün köşe koto denklemini elde ederiz - sürü bir noktada bulunur; ve simetri ekseni O eksenidir Şekil. Bölgenin sınırı aşağıdaki denklemlerle verilmiştir: koordinatların orijininden ve parabolün üst dalından geçen düz bir çizgi Böylece entegrasyon bölgesi Şekil 7.
8 İntegral sınırlarını belirlemek için sınır çizgilerinin kesişme noktalarının koordinatlarını bulacağız. Bunu yapmak için denklem sistemini çözeceğiz; Dolayısıyla A; İÇİNDE; İntegral sırasını değiştirirken değişken üzerinden dış integrali alacağız. Dolayısıyla bölgeyi kesen ve Ox eksenine paralel bir doğru çizeceğiz. Yani, integral alma sırasını değiştirerek şunu elde ederiz: f f f Burada, integral alma sırasını değiştirmek hesaplamaları basitleştirir çünkü iki integrali hesaplamak yerine sadece bir tane hesaplamanız gerekecektir. Örnek Hesaplama; ; alanın çizgilerle sınırlandığı yer Çözüm Şekil 9'daki alanı oluşturalım: O eksenine paralel bir doğru ve koordinatların orijininden geçen düz çizgiler İntegrali hesaplamak için çift katlı integralden tekrarlanan integrale geçelim. Alan bir eşitsizlik sistemi ile tanımlanabildiği için: Şekil 9 İntegral değişken üzerinden gerçekleştirildiğinden, ilk olarak iç integrali sabit bir değer olarak kabul ederek hesaplıyoruz: Şimdi ortaya çıkan dış integrali hesaplamak kalıyor:
9 Örnek Hesaplama Çözümü Bir bölge oluşturun: O ekseni, O eksenine paralel bir düz çizgidir, koordinatların orijininden geçen düz bir çizgidir Şekil. Düz çizgiler ve A noktasında kesişir; Çift katlı integrale geçip onu hesaplayarak, Şekil 9'daki indirgeme formüllerine göre çizgilerle sınırlı olup olmadığını elde ederiz.
10 Bağımsız çözüm problemleri Alanın aşağıdaki çizgilerle sınırlı olması durumunda f'nin indirgendiği tekrarlı integrallerde integrasyon sınırlarını düzenleyin: a; B; V; G; d ABC üçgeni burada A; İÇİNDE; İLE; Entegrasyon sırasını değiştirin: a f ; bf; f'de; g f Alanın belirtilen çizgilerle sınırlı olduğunu varsayarak çift katlı integralleri hesaplayın: a; 7; B; ; V; ; g e; 6 Cevap a f ; bf; gf'de; daf; bff; f'de; gfa; 7b; V; f 6 g ef;
11 KUTUPLU KOORDİNATLARDA ÇİFT INTEGRAL Düzlemde hem Kartezyen hem de kutupsal koordinat sistemi verilmişse ve kutup, koordinatların orijini ile çakışıyorsa ve kutupsal eksen Ox ekseni ile aynı hizadaysa, kutupsal koordinatlara gitmek için Şekil 1'deki formülleri kullanın. Ayrıca alan α β ışınları ve eğrilerle sınırlıysa Şekil f β α f Örneklerin çözümü Örnek Hesapla > Çözüm Şekilde bir bölge oluşturalım: koordinatların orijininden geçen düz çizgilerle yarıçaplı bir daire. bir dairenin parçası olduğundan kutupsal koordinatlara gitmek uygundur. Bu durumda kutup O noktasıyla uyumludur; ve kutupsal eksen O ekseni boyunca olsun. O zaman alan çizgilerle sınırlanır Şekil Şimdi alanı kutupsal koordinat sisteminde tanımlamamız gerekir. Alanın içindeki açı cm'den cm'ye kadar değişir Şekil Düz k O eksenine eğiktir
12 tanjantı k'ye eşit olan bir açıda Bu nedenle tg ; tg Buradan; Böylece, bölgenin içinde, O kutbundan çıkan ve kesişen bir ışın, bölgeyi kutupsal koordinatlarda denklemi şu şekilde olan bir daire boyunca terk eder. Böylece bölge bir eşitsizlik sistemi ile tanımlanır: Artık ayarlamak kolaydır Tekrarlanan integralin limitleri ve bunu hesaplayın Örnek Halkanın olduğu yerde e'yi hesaplayın Çözüm Bölge 9 ve 9 numaralı dairelerle sınırlı olduğundan, Şekil. kutupsal koordinatlara geçmek uygundur: O zaman sınır denklemleri şu şekli alacaktır; 9 Şekil Tekrarlanan integralde integralin sınırlarını belirlemek için, bölge içinde açının tüm değerleri aldığını not edelim. Bölgeyi kesen koordinatların orijininden bir ışın çizelim. Bölgeye bir çizgi boyunca girer. ve çizgi boyunca ayrılır Böylece: Sonra.
13 9 9 9 eee eee eee eee Örnek Eşitsizliklere göre belirlenip belirlenmediğini hesaplayın: Çözüm Bir bölge oluşturalım Bunu yapmak için sınır denklemini dönüştürüyoruz: Yani sınır, bir noktada merkezi olan yarıçaplı bir dairedir; O zamandan beri dairenin üst yarısı Şekil Kutupsal koordinatlara geçelim: Şekil Kutupsal koordinatlardaki sınır denklemi şu şekli alacaktır: Alan tamamen ilk çeyrekte yer almaktadır dolayısıyla kutupsal koordinatlarda alan şu şekildedir: eşitsizlikler tarafından verilir Şimdi çift katlı integrali hesaplayabiliriz
14 Bağımsız çözüm için problemler Kutupsal koordinatlara geçerek hesaplayın: burada dairenin üst yarısı 6 burada alan eşitsizlikleri karşılıyor burada alan çizgilerle 9 6 sınırlanıyor burada çizgiler 6 ile sınırlanıyor burada alan eğrilerle sınırlanıyor Cevaplar; ; ; ; ÇİFT İNTEGRAL UYGULAMALARI Çift katlı integral aşağıdakilerin hesaplanmasında kullanılır: ve alanla sınırlı bir düzlem şeklinin alanı: S; b yukarıdan sürekli bir yüzey f ile aşağıdan bir düzlemle ve yandan O düzlemi üzerinde bir alanı kesen düz bir silindirik yüzeyle sınırlanan silindirik bir cismin hacmi:
15f; f denklemiyle verilen yüzey alanında, O düzlemine izdüşümü şu bölgedir: σ Ek olarak, mekanikte çift katlı integraller hesaplamak için kullanılır: ve O düzleminin bölgesini kaplayan düz bir plakanın kütlesi ve değişken bir yüzey yoğunluğuna sahip olan γ γ: M γ; b plakanın O ve O eksenlerine göre istatistiksel momentleri: ; Mγ; Plakanın ağırlık merkezinin koordinatlarında M γ: γ M c; M γ Örneklerin çözümü м M M γ γ 6 Örnek Çizgilerle sınırlanan bölgenin alanını bulun Çözüm Bölgeyi oluşturalım Denklem bir parabolü tanımlar, koordinatların orijininden geçen düz bir çizginin denklemi Şekil Bulmak için bu doğruların kesişme noktalarında denklem sistemini çözüyoruz: Buradan Sonra Böylece düz çizgi parabolü noktalarda kesiyor; ve A; Formülü kullanarak S Şekil Örnek İlk dairenin dışındaki çizgilerle sınırlanan bir şeklin alanını bulun;
16 Çözüm Denklem, merkezi koordinatların orijininde olan yarıçaplı bir daireyi belirtir Denklem, merkezi noktada olan yarıçaplı bir daireyi belirtir Denklem sistemini birlikte çözelim ± Yani; A; B AmBn bölgesi eşitsizliklerle belirtilebilir Formül 6'yı kullanarak S Örnek Koordinat düzlemleri ve bir düzlemle sınırlanan bir cismin hacmini bulun Çözüm Şekil 7'deki cismi ve onun O düzlemine izdüşümünü oluşturalım Şekil 6
17 Formüle göre Şek. 7 Şek. Örnekte, alan, Şek.'de gösterilen OAB üçgenidir ve yüzey, buradan itibaren düzlemin denklemi ile belirlenir. Bu Örnek Koordinat düzlemleriyle sınırlı bir cismin hacmini bulun. düzlemin ve yüzeyin Çözümü Gövde Şekil 9'da gösterilmektedir. Düzlem O eksenine paralel uzanır; tepe noktası noktada olan bir paraboloit;; Cismin O düzlemine izdüşümü ABO üçgenidir, şekil AB'dir, düzlemin düzlemle kesişme çizgisidir, dolayısıyla AB düz çizgisinin denklemi: buradan 7
18 Formülü kullanma Şekil 9 Şekil silindirle 6 Örnek Bir paraboloit ve düzlemlerle sınırlanmış bir cismin hacmini bulun ve Çözüm Cisim Şekilde gösterilmiştir. İntegrasyon sınırlarını belirlemede kolaylık sağlamak için, cismin izdüşümünü oluşturuyoruz. vücut O düzlemine doğru Şek. Formülü kullanarak Şek. Şek.
19 7 6 Örnek 6 Yüzeylerle sınırlanan bir cismin hacmini bulun 7 Çözüm Bu cisim iki paraboloidle sınırlanmıştır Şekil. Paraboloitlerin kesişim çizgisi bir denklem sistemi tarafından belirlenir İlk denklemden Yani kesişim çizgisi bir dairedir düzlemde bulunan yarıçapın yarıçapı: Bu çizginin O düzlemine izdüşümü de bir dairedir, dolayısıyla kutupsal koordinatlara geçmek uygundur Şekil. Bir cismin hacmi, cisimlerin hacimleri arasındaki fark olarak hesaplanabilir. iki silindirik gövde: Örnek 7 Silindir içindeki bir kürenin yüzey alanını bulun 9 Çözüm Bir silindir, kürenin yüzeyinde O düzlemine göre simetrik olan iki parçayı keser Şekil. Simetri nedeniyle, yalnızca üst “başlığın” yüzey alanını hesaplayın ve sonucu iki katına çıkarın 9
20 Hesaplamak için formülü kullanıyoruz Kısmi türevler içerdiğinden hesaplıyoruz ve dolayısıyla bir kürenin denkleminden elde ediyoruz Sonra Şekil Böylece σ formülüne göre yüzeyin O düzlemine izdüşümü dairesine gitmek uygundur. kutupsal koordinatlara Kutupsal koordinat sisteminde, bir dairenin denklemi şöyle görünür: Kutupsal koordinatlarda σ 9, dolayısıyla 9 kabul edilecektir Yalnızca üst “başlığın” alanını dikkate aldığımız için, tüm yüzey alanı σ'ya eşittir. σ n Örnek Homojen bir ABC plakasının ağırlık merkezini bulun: A;- B; C; ;- Çözüm Ağırlık merkezinin koordinatlarını hesaplamak için aşağıdaki formülleri kullanacağız: 6 Plaka homojen olduğundan yüzey yoğunluğu γ sabittir, dolayısıyla formüller q formunu alacaktır; ts
21 Şekildeki şekilden plakanın yamuk şeklinde olduğu ve O eksenine göre simetrik olduğu açıkça görülmektedir. Bu nedenle BC ve A doğrularının denklemlerini a denklemini belirleyen formülü kullanarak yazalım. Verilen iki noktadan geçen düz çizgi: c BC: ; A: Şekil Şimdi koordinatı belirleyen kesrin pay ve paydasını ayrı ayrı hesaplayalım: q 9 Payda, ABC yamuğunun alanına ve ABC yamuğunun alanına eşit bir integral içerir. Dolayısıyla h ; bu AB C integralini doğrudan hesaplayabilirsiniz. Böylece c; q Örnek 9 Her noktadaki yoğunluk b noktasının ordinatına eşitse elipsin üst yarısının kütlesini bulun Çözüm Her noktadaki yoğunluk γ ordinatına eşittir M γ formülüne göre Üst yarısı için elips, Şekil 6 b dolayısıyla a Şekil 6
22 M a a a a b a a a a b a a a b a a a b Bağımsız çözüm problemleri a ab Çizgilerle sınırlanan şeklin alanını bulun: a; B; bir ; g a a; d Aşağıdaki yüzeylerle sınırlanan cismin hacmini bulun: a; B; bir; d Belirtilen yüzeyin alanını bulun: birinci oktantın içine alınmış düzlem 6'nın kısmının a; b silindir a tarafından kesilen a düzleminin bir kısmı; silindir içindeki bir paraboloitte; Parabolik bir silindir ve bir düzlem tarafından kesilen bir paraboloidin g'si ABC yamuğunun ağırlık merkezini bulun, burada A; B; C; ; her noktadaki yoğunluk bu noktanın apsisine eşitse Bir parabol ve bir düz çizgiyle sınırlanan homojen bir şeklin ağırlık merkezini bulun 6 Her noktadaki yüzey yoğunluğu orantılıysa yarıçaplı dairesel bir plakanın kütlesini bulun dairenin merkezinden uzaklığına kadar Cevaplar a; B; V; g a a; d 6 a 6; B; bir; g a a
23a; b bir; V; g c c c c 6 6 k KARTEZYEN KOORDİNATLARDA ÜÇLÜ İNTEGRALLERİN HESAPLANMASI Üç katlı bir integrali hesaplamak için, üçlü bir integral olarak temsil edilir: Örneklerin çözümü Örnek f b a f f'den üçe gidin ve alan aşağıdakilerle sınırlıysa integralin sınırlarını ayarlayın: bir düzlem ve koordinat düzlemleri; b konisi ve h düzlemi; bir top içinde Çözüm a Bir bölge oluşturalım ve bu bölgenin O düzlemine izdüşümü Şekil 7 Düz AB, düzlem ile düzlemin kesişme çizgisidir, dolayısıyla denklemi Dolayısıyla bu OAB'dir Şekil 7 Şekil Şekilden O eksenine paralel ve OAB üçgenini kesen düz bir çizgi çizdiğimizde, onun çizgi boyunca girip çıktığını fark ediyoruz.
24 Değişimin sınırlarını bulmak için O eksenine paralel ve alanı kesen düz bir çizgi çiziyoruz Şekil 7 Yüzey boyunca alana girer ve yüzey boyunca çıkar. Böylece alan bir sistemle tanımlanabilir. eşitsizlikler 6 dolayısıyla f f 6 b Üçlü integralin sınırlarını ayarlamak için alanı ve onun O bölgesi düzlemine izdüşümünü oluştururuz Şekil 9 Alanı sınırlayan çizginin denklemi, h h Şekil 9 denklem sisteminin çözülmesiyle elde edilir: merkezi koordinatların orijininde olan, yarıçapı h olan bir çemberdir. O ve O'ya kesişen düz çizgiler çizersek, h h h h h eşitsizlik sistemi tarafından tanımlanan şeyi elde ederiz. Dolayısıyla h h h h f f
25 Üçlü bir integralde farklı bir integral alma sırası seçebilirsiniz, o zaman doğal olarak integralin sınırları da değişecektir. Örneğin, orijinal integrali c f şeklinde düşünelim. İntegralin sınırlarını belirlemek için düzleme izdüşümü yapacağız. O ve sırasıyla O ve O'ya paralel ve kesişen düz çizgiler çizin ve Şekil. Bu durumda eşitsizliklerle verilir: h dolayısıyla h f f Şekil c Alanı ve O düzlemine izdüşümünü oluşturalım Şekil Şekil Çizimden bu açık
26 f f f f Örnek Cismin bir düzlem ve bir koninin koordinat düzlemleriyle sınırlı olup olmadığını hesaplayın Çözüm Cismi ve onun O düzlemine izdüşümünü oluşturalım Şekil. Çizimden eşitsizliklerle tanımlandığı açıktır: Şekil Böylece 6 6
27 Bağımsız çözüme yönelik problemler f'den üçlü integrale gidin ve cisim sınırlıysa integralin sınırlarını belirleyin: a bir elipsoidle; 9 b paraboloit ve düzlem; koordinat düzlemlerinde ve bir düzlemde 6 Cismin düzlemlerle ve bir küreyle sınırlı olup olmadığını hesaplayın Cismin düzlemlerle sınırlı olup olmadığını hesaplayın Hesaplayın ve koni Cevaplar 9 Cisim a f düzlemleriyle sınırlıysa; bf; f 6 ÜÇLÜ INTEGRAL SİLİNDİRİK VE KÜRESEL KOORDİNATLARDAKİ DEĞİŞKENLERİN DEĞİŞİMİ Silindirik koordinatlara geçiş formülleri Şekil: ; ; ; Küresel koordinatlara geçiş formülleri θ r Şekil: r θ ; rθ; rθ; r θrθ Burada; θ; r7
28 Örneklerin çözümü Örnek Şekil hesaplayın, eğer bir koni ve bir düzlem ile sınırlıysa Çözüm Cisim Şekilde gösterilmiştir. Koni ile düzlemin kesişme çizgisi aşağıdaki denkleme sahiptir. Böylece cismin O daire düzlemine izdüşümü Şekil 6 Şekil 6 Silindirik koordinatlara geçelim: ; ; ; Bu koordinatlarda, Şekil 6'da gösterilen dairenin denklemi, koninin ve cismin denklemi eşitsizliklerle verilmektedir; ; Bu yüzden
29 v Örnek Cismin yüzeylerle sınırlı olup olmadığını hesaplayın Çözüm Bir bölge oluşturun; düzlem Bir yüzey oluşturmak için denklemi dönüştürürüz: Bu denklem, tabanında merkezi noktası olan yarıçaplı bir daire bulunan dairesel bir silindiri tanımlar; Dolayısıyla entegrasyon bölgesi bir silindirdir, Şekil 7. Bu nedenle silindirik koordinatların kullanılması uygundur. Bu koordinatlarda, entegrasyon bölgesini sınırlayan silindirik yüzeyin denklemi şu şekilde olacaktır: Buna dayanarak, bölge bir eşitsizlik sistemi ile tanımlanabilir; ; Şekil 7 9
30 Örnek Cismin topun üst yarısı olduğunu hesaplayın Çözüm Burada entegrasyon bölgesi topun parçası olduğundan, küresel koordinatlara gitmek uygundur: r r r r r r r r r r r r r θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ Bağımsız çözüm problemleri Sınırlı yüzeyler olup olmadığını hesaplayın Yüzeylerin nerede sınırlandığını hesaplayın
31 Hesapla Bir topun yüzeyleri ile sınırlıysa hesaplayın Cevaplar ÜÇLÜ İNTEGRALLERİN UYGULAMALARI Üç katlı integral aşağıdakileri hesaplarken kullanılır: ve bir cismin hacmi Ω: ; 7 Ω b değişken hacimsel yoğunluğa sahip Ω alanını kaplayan vücut kütlesi γ: M γ ; Ω, vücudun ağırlık merkezinin koordinatlarında Ω: q γ M Ω q γ 9 M Ω q γ M Ω, burada M, vücudun kütlesidir. Eğer vücut homojense, o zaman formül 9'a γ koyabiliriz. ; M Örneklerin çözümü Örnek Bir silindir ve düzlemlerle sınırlanan bir cismin hacmini bulun Çözüm Cisim ve onun O düzlemine izdüşümü Şekil'de gösterilmektedir. Şekil. A ve B noktalarının koordinatlarını bulmak için denklem sistemini çözüyoruz :
32±A; B; Böylece Ω bölgesi bir eşitsizlik sistemi ile tanımlanır; ; 7 Ω formülünü kullanarak Örnek Her noktadaki yoğunluk γ ise, düzlemlerle sınırlanmış bir cismin kütlesini bulun Çözüm Bir Ω cismi ve onun O düzlemine izdüşümünü oluşturalım Şekil 9 Şekil 9 Düzlem, düzlemi bir düz boyunca kesiyor çizgi Sistemi çözerek A noktasının koordinatlarını elde ederiz; Böylece Ω gövdesi bir eşitsizlik sistemi ile tanımlanır; ; Vücut kütlesi formülünü kullanarak M Ω Örnek 9 düzlemleri ve parabolik silindir tarafından sınırlanan bir cismin kütlesini hesaplayın; eğer her noktadaki yoğunluk apsis ile orantılıysa ve O düzleminden bir birim uzaklıkta şuna eşitse:
33 Çözelti Yoğunluğu apsis ile orantılıdır; dolayısıyla k γ O düzleminden birim uzaklıkta yoğunluk eşittir; dolayısıyla γ için Sonra k k Böylece γ Ω cismini ve onun O düzlemine izdüşümünü oluşturun Şekil Şekil A noktasının koordinatlarını bulmak için denklem sistemini çözün; 9 A Böylece bölge Ω Ω eşitsizlik sistemi ile tanımlanabilir. 9: Formüle göre cismin kütlesi Ω M'ye eşittir Örnek Alt yarısıyla sınırlanan bir cismin ağırlık merkezinin koordinatlarını bulun Kürenin ve bir paraboloidin her noktadaki yoğunluğu O eksenine olan mesafenin karesiyle orantılıysa
34 Çözüm Bir cisim oluşturalım. Paraboloidin tepe noktası bir noktadır; ; Denklem, merkezi bir noktada bulunan yarıçaplı bir küreyi tanımlayacak biçimde dönüştürülebilir; ; Yani cisim Şekilde gösterilen forma sahiptir. Bu cismin O düzlemine izdüşümü bir dairedir. Denklem sistemi çözülerek elde edilebilir. Düzlemde kesişim çizgisinin denklemi şu şekildedir. Ω gövdesinin düzleme izdüşümünün denklemi aynı formdadır Ω Şekil. Daire hesaplama sırasında uygun olduğundan, silindirik koordinatlara gidin; ; Bu koordinatlarda Ω sınırının denklemi şu şekildedir; ve açı şu koşulu karşılar: Silindirik koordinatlarda bir paraboloit denklemi buradan Bir kürenin denklemi: ± Alt yarı için Problem koşullarına göre değişken yoğunluk, O ekseninden γ k olan uzaklığın karesi ile orantılıdır. silindirik koordinatlar γ k Cisim O eksenine göre simetrik olduğundan, ağırlık merkezinin bu eksen üzerinde olduğu açıktır; q q'yu hesaplamak için formül 9'u kullanırız: q γ M Ω İlk önce M cismin kütlesini hesaplayalım [formül ]:
35 6 k k k k k k k M γ Ω Ω Ω Şimdi Ω Ω Ω γ k k k k k k k k k k formülüne göre hesaplayalım. Yani söz konusu cismin ağırlık merkezinin koordinatları vardır; ; 7
36 Bağımsız çözümlü problemler 6 Aşağıdakilerle sınırlanan bir cismin hacmini bulun: bir düzlem; b paraboloit ve düzlem; yüzeylerde ve 6 Sınırlı bir cismin kütlesini bulun: a yoğunluk γ k ise kürelere göre; yoğunluk γk ise b yüzeyleri; Bir koni ve b düzleminde yoğunluk noktanın ordinatı ile orantılıysa ve O düzleminden bir birim uzaklıkta ise γ 6'ya eşitse a düzlemleriyle sınırlanan homojen bir cismin ağırlık merkezinin koordinatlarını bulun Cevaplar 6a; B; 6 9 k γb 6 a k'de; B; 6 6°C'de; 6
37 Seçenek EK BİREYSEL ÖDEV İÇİN SEÇENEKLER Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun Silindirin içine alınmış bir silindirin yüzey alanını bulun Yüzeylerle sınırlanmış bir cismin hacmini bulun Bir cismin kütlesini bulun herhangi bir noktadaki yoğunluk bu noktanın uygulamasına eşitse küre ve bir paraboloid Seçenek Bir çizgi ve bir yarım dalga sinüzoidle sınırlanan düz bir şeklin ağırlık merkezini bulun Bir koninin yüzey alanını aşağıdakilerle keser: düzlemler Yüzeylerle sınırlanan bir cismin hacmini bulun Herhangi bir noktadaki yoğunluk, noktadan düzleme olan mesafeye eşitse, birinci oktantta yer alan yarıçaplı bir topun bir kısmı ile sınırlanan bir cismin kütlesini bulun O Seçenek Bul çizgilerle sınırlanan düz bir şeklin ağırlık merkezi Silindirin içindeki koninin yüzey alanını bulun 9 Yüzeylerle sınırlanan bir cismin hacmini bulun 9 9 Yüzeyler 9 ile yüzeyler arasında küresel bir katmanla sınırlanan bir cismin kütlesini bulun 6 eğer her noktadaki yoğunluk, noktadan koordinatların orijinine olan uzaklıkla ters orantılıysa Seçenek Çizgilerle sınırlanan düz bir şeklin ağırlık merkezini bulun 6 > Silindirin içindeki yüzey alanını bulun 6 Bir cismin hacmini bulun yüzeylerle sınırlanmış gövde 7
38 Her noktadaki yoğunluk, noktadan silindirin simetri eksenine olan mesafenin karesine eşitse, yüksekliği yarıçaplı dik dairesel bir silindirle sınırlanan bir cismin kütlesini bulun Seçenek Bir cismin ağırlık merkezini bulun yarıçapı ve O eksenine göre simetrik olarak yerleştirilmiş ve birbirlerini açı oluşturan iki ışınla koordinatların kökeni merkezli bir daire ile sınırlanan düz şekil Silindirin içinde yer alan bir koninin yüzey alanını bulun Sınırlı bir cismin hacmini bulun yüzeylere göre Koordinat düzlemleri ve düzlem 6 ile sınırlanan bir cismin kütlesini bulun, eğer her noktadaki yoğunluk bu noktanın apsisine eşitse Seçenek 6 O ekseni ve düzlemin üst kısmı tarafından sınırlanan düz bir şeklin ağırlık merkezini bulun elips b a Silindirin düzlemlerle kesilen yüzey alanını bulun Yüzeyler 6 ile sınırlanan bir cismin hacmini bulun Her noktadaki yoğunluk bu noktanın uygulamasına eşitse, yüzeyler 6 ile sınırlanan bir cismin kütlesini bulun Seçenek 7 Kardioidle sınırlanmış düz bir şeklin ağırlık merkezini bulun 7 Silindirle kesilmiş bir koninin yüzey alanını bulun Talimatlar Kutupsal koordinatlara gidin Yüzeylerle sınırlanmış bir cismin hacmini bulun Sınırlı bir cismin kütlesini bulun yüzeylere göre > yoğunluk noktanın ordinatına eşitse Seçenek p çizgileriyle sınırlanan düz bir şeklin ağırlık merkezini bulun
39 Silindir içindeki bir paraboloidin yüzey alanını bulma Yüzeylerle sınırlanan bir cismin hacmini bulma 6 Her noktadaki yoğunluk eşitse yüzeylerle sınırlanan bir cismin kütlesini bulma Seçenek 9 Bir dairenin ağırlık merkezini bulma çizgilerle sınırlanan şekil 9 9 > Bir küre ve bir paraboloit ile sınırlanan bir cismin yüzey alanını bulun Silindirin dışındaki 6 9 yüzeylerle sınırlanan bir cismin hacmini bulun Aralarında küresel bir katmanla sınırlanan bir cismin kütlesini bulun yoğunluk, noktanın koordinatların orijininden uzaklığıyla ters orantılıysa yüzeyler 6 Seçenek Koordinatların orijininden ve A noktasından geçen bir çizgi ve düz çizgi OA ile sınırlanan düz bir şeklin ağırlık merkezini bulun; Bir silindir tarafından kesilen bir kürenin yüzey alanını bulun Yüzeylerle sınırlanan bir cismin hacmini bulun; iç silindirler Yoğunluk topun merkezinden uzaklığın küpüyle orantılıysa ve birim mesafede γ'ya eşitse, yarıçapı olan bir topla sınırlanan bir cismin kütlesini bulun; Seçenek Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun 6 Düzlemler arasındaki silindirin yüzey alanını bulun Yüzeylerle sınırlanmış bir cismin hacmini bulun Yoğunluk varsa silindirik bir yüzey ve düzlemlerle sınırlanmış bir cismin kütlesini bulun 9 noktasının ordinatına eşittir
40 Seçenek Kardioidle sınırlanan düz bir şeklin ağırlık merkezini bulun Bir silindirin içine alınmış bir topun yüzey alanını bulun Yüzeylerle sınırlanan bir cismin hacmini bulun Bir topun oktantıyla sınırlanan bir cismin kütlesini bulun Her noktadaki yoğunluk bu noktanın uygulamasına eşitse koordinat düzlemleri ve bir düzlemle Seçenek Çizgilerle sınırlanan düz bir şeklin ağırlık merkezini bulun Bir silindir ile bir düzlem arasına alınmış bir paraboloidin alan yüzeyinin bulunması c a b Bul Yoğunluk noktanın koordinatlarının karelerinin toplamına eşitse, bir paraboloit ve bir düzlemle sınırlanmış bir cismin kütlesi Seçenek Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun Bir silindirin yüzey alanını bulun O düzlemi ile yüzey arasına alınmış Yüzeylerle sınırlanan bir cismin hacmini bulun Yoğunluk, noktadan silindirin eksenine olan mesafenin karesiyle orantılıysa, silindir 6 ile sınırlanan bir cismin kütlesini bulun Seçenek Bul çizgilerle sınırlanan düz bir şeklin ağırlık merkezi α α tg tg Silindirin içinde bulunan bir koninin yüzey alanını bulun Yüzeylerle sınırlanan bir cismin hacmini bulun
41 Yüzeylerle sınırlanmış bir cismin kütlesini bulun > yoğunluk noktanın ordinatına eşitse Seçenek 6 Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun 6 Silindirlerin içindeki bir topun 6 yüzey alanını bulun Yüzeylerle sınırlanan bir cismin hacmini bulun b a a b Yoğunluk noktanın uygulama alanına eşitse yüzeylerle sınırlanan bir cismin kütlesini bulun Seçenek 7 Her iki noktadaki yoğunluk da bir bacağı olan bir ikizkenar dik üçgenin ağırlık merkezini bulun nokta dik açının tepe noktasına olan mesafenin karesiyle orantılıdır Silindir tarafından kesilen koninin yüzey alanını bulun Talimatlar Kutupsal koordinatlara gidin Yüzeylerle sınırlanmış bir cismin hacmini bulun 9 Bir cismin kütlesini bulun yarıçaplı topun yoğunluğu, topun merkezinden olan mesafenin küpüyle orantılıysa ve birim mesafe başına γ Seçenek Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun Bir cismin yüzey alanını bulun birinci oktantın içine alınmış paraboloid Bir paraboloid bir düzlemle sınırlanmıştır 6 Yüzeylerle sınırlanmış bir cismin hacmini bulun 6 Her noktadaki yoğunluk aşağıdakilere eşitse, yarıçapı birinci oktantta yer alan bir parçanın kütlesini bulun düzlemden uzaklık O Seçenek 9 Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun Bir küre ve paraboloidle sınırlanmış bir cismin yüzey alanını bulun
42 Yüzeylerle sınırlanmış bir cismin hacmini bulun Yoğunluk, noktanın silindir tabanının merkezinden uzaklığının karesine eşitse, yüksekliği yarıçaplı dik dairesel bir silindirle sınırlanan bir cismin kütlesini bulun Seçenek Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun > Bir silindir tarafından kesilmiş bir kürenin 9 yüzey alanını bulun Yüzeylerle sınırlanmış bir cismin hacmini bulun Yoğunluk şu şekildeyse yarıçaplı bir topun kütlesini bulun: merkezden uzaklığın küpüyle orantılı ve birim uzaklıkta γ Seçenek Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun ± tg 6 Silindirin içindeki silindirin yüzey alanını bulun Bul silindir içindeki yüzeylerle sınırlanan bir cismin hacmi Yoğunluk, noktalardan düzleme olan mesafeyle orantılıysa, iki topun ortak kısmıyla sınırlanan bir cismin kütlesini bulun. O Seçenek Aşağıdakilerle sınırlanan düz bir şeklin ağırlık merkezini bulun: a kardioid Düzlemlerle kesilmiş bir koninin yüzey alanını bulun Silindirin dışındaki yüzeylerle sınırlanan bir cismin hacmini bulun 6 Her noktadaki yoğunluk varsa, yarıçaplı bir topun birinci oktantta yer alan bir kısmının kütlesini bulun O düzlemine olan mesafeye eşittir
43 Seçenek Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun Bir silindir ile bir düzlem arasına alınmış bir paraboloidin 6 yüzey alanını bulun Yüzeylerle sınırlanmış bir cismin hacmini bulun Küresel bir cisimle sınırlanmış bir cismin kütlesini bulun yoğunluk başlangıç noktasına olan uzaklıkla ters orantılıysa yüzeyler arasındaki katman 6 Seçenek Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun 9 Silindirin içindeki yüzey alanını bulun Yüzeylerle sınırlanmış bir cismin hacmini bulun Kütleyi bulun Yoğunluk noktanın koordinatlarının karelerinin toplamına eşitse, bir paraboloit ve bir düzlemle sınırlanmış bir cismin Seçenek Çizgilerle sınırlanmış düz bir şeklin ağırlık merkezini bulun İçerideki bir koninin yüzey alanını bulun bir silindir Yüzeylerle sınırlanan bir cismin hacmini bulun Yoğunluk noktadan O düzlemine olan mesafeyle orantılıysa ortak bir parçayla sınırlanan bir cismin kütlesini iki topla bulun
44 İÇİNDEKİLER KARTEZYEN KOORDİNATLARDA ÇİFT İNTEGRALLERİN HESAPLANMASI KUTUSUZ KOORDİNATLARDA ÇİFT İNTEGRAL ÇİFT İNTEGRAL UYGULAMALARI KARTİZİT KOORDİNATLARDA ÜÇLÜ İNTEGRALLERİN HESAPLANMASI SİLİNDİRİK VE KÜRESEL KOORDİNATLARDA ÜÇLÜ DEĞİŞKENLERİN DEĞİŞTİRİLMESİ 7 6 ÜÇLÜ İNTEGRALLERİN UYGULAMALARI BİREYSEL ÖDEV İÇİN TEGRALS EK SEÇENEKLERİ 7 Eğitim baskısı ÇOKLU İNTEGRAL problemleri ve alıştırmalar Metodolojik talimatlar Karpilova Olga Mikhailovna tarafından derlenmiştir Editör Yu N Litvinova Derleme Yu N Litvinova Basım için imzalanmıştır Format 6x/6 Ofset kağıt Ofset baskı Koşul l 7 Kopya dolaşımı Sipariş Art S- 9/ Samara State Aerospace University 6 Samara Moskovskoe Highway Samara Devlet Havacılık ve Uzay Üniversitesi Yayınevi 6 Samara Moskovskoe Otoyolu
Cos, sin, J dd dd d d 5 zdd zddz ddz'yi hesaplayın, burada z yüzeyinin dış tarafı z düzlemi tarafından kesiliyor Çözüm Yüzey, z denklemiyle açıkça tanımlanan bir paraboloittir. Bu nedenle
DEVLET YÜKSEK MESLEKİ EĞİTİM KURUMU "Belarus-Rus Üniversitesi" "Yüksek Matematik" YÜKSEK MATEMATİK Bölümü. MATEMATİK. MATEMATİK (ÖZEL BÖLÜMLER). MATEMATİKSEL ANALİZ
YÜKSEK MATEMATİK DERSİNDE HESAPLAMA GÖREVLERİ İÇİN METODOLOJİK TALİMATLAR "SADECE DİFERANSİYEL DENKLEMLER SERİLERİ ÇOKLU İNTEGRALLER" BÖLÜM III KONU ÇOKLU İNTEGRALLER İÇİNDEKİLER İkili ve üçlü hesaplamalar
Rusya Federasyonu Ulaştırma Bakanlığı Federal Devlet Bütçe Yüksek Öğrenim Eğitim Kurumu "Rusya Ulaştırma Üniversitesi (MIIT)" ITTSU "Yüksek ve Bilgisayar" Dairesi
Rusya Federasyonu Eğitim ve Bilim Bakanlığı Federal Devlet Bütçe Yüksek Mesleki Eğitim Kurumu "Sibirya Devlet Endüstri Üniversitesi"
PRATİK DERS 9 Kutupsal koordinatlarda çift katlı integralin hesaplanması Çift katlı integrallerin uygulamaları Çift katlı integral hesaplanırken sıklıkla kullanılan değişkenlerin değişiminin özel bir durumunu ele alalım.
Çift katlı integraller Problem çözme örnekleri 1. G, eğrilerle sınırlanan bir bölge ise, çift katlı f(x, y) dx dy çift katlı integralini iki yolla (formül (1) ve formül (2) ile) tekrarlanan bire azaltın. x = 1, y = x 2, y =
Vücut kütlesinin silindirik koordinatlarda üçlü integral yoluyla ifadesi Tanımlar ve problemlerin çözümü için formüller Tanım O ekseni boyunca yönlendirilmiş silindirik bir kiriş Şekil. Sınırlı bir G cismine denir
Belarus Cumhuriyeti Eğitim Bakanlığı BEYAZ RUSYA ULUSAL TEKNİK ÜNİVERSİTESİ Mühendislik Matematiği Bölümü N.A. Kondratyeva O.G. Vishnevskaya N.K. Prikhach MATEMATİK Metodolojik el kitabı
Kılavuz, öğrenimlerinin ikinci yılındaki yarı zamanlı KSTU öğrencilerine yöneliktir. Kılavuz aşağıdaki konuları kısa ve erişilebilir bir biçimde kapsamaktadır: Çoklu integraller, Eğrisel integraller, Seriler, Olasılık teorisi.
Rusya Federasyonu Bilim ve Eğitim Bakanlığı Moskova Devlet Jeodezi ve Haritacılık Üniversitesi AV Aristarkhova, NG Babaeva Yüksek matematikte bireysel ödevler ÇOKLU İNTEGRALLER
“INTEGRAL HESABI” KONUSUNDA SORUNLU BANKA * İntegral sırasını değiştirin + d d * Çizgilerle sınırlanan düz bir bölgenin alanını bulun =, =, = * (D) + acctg d'yi hesaplayın, burada) +, + 9, = (D bölgesi,
RUSYA FEDERASYONU KÜLTÜR BAKANLIĞI FEDERAL DEVLET BÜTÇE YÜKSEK MESLEKİ EĞİTİM KURUMU ST. PETERSBURG DEVLET SİNEMA ÜNİVERSİTESİ VE
Parça. Matematikte örnek sınav problemleri A. Üç nokta için en basit görevler.. Arcsin integrallerini hesaplayın e) ISiA II dönemi ve 9 gr. i) 6 n j) 5 6 5 g) 6 d) cos h) z arcsin z. Türevi Hesapla
RUSYA FEDERASYONU ULAŞTIRMA BAKANLIĞI FEDERAL DEVLET BÜTÇE EĞİTİM YÜKSEKÖĞRETİM KURUMU "RUSYA ULAŞTIRMA ÜNİVERSİTESİ (MIIT)" Ulaştırma Teknolojisi Enstitüsü
3. bölge (D) Bizim durumumuzda n, XOY düzleminin normal vektörüdür, bunlar n k ( ) = ϕ, ϕ, Sonra = = ve n ( ) cos γ =, + + (ϕ) (ϕ) (ϕ) (ϕ) dq = + + dd Not Eğer yüzey (Q) doğru yönde ise
MATEMATİK PROBLEMİ (teknik fakülteler, yarıyıl) 7 İntegraller İntegralleri bulun d d sin + d + + d + d + d 7 (+) d + + 8 d 9 cos d cos + d cos d + 8 d 9 d d + d 9 + d + 7 tg d 8 cosd çünkü sin 9 d
DERS N 45 Kutupsal, silindirik ve küresel koordinatlarda çoklu integraller Çoklu integrallerin uygulamaları Kutupsal koordinatlarda çift katlı integral Silindirik ve küresel koordinatlarda üçlü integral
Bölüm. Çoklu integraller.. Ders... Çift katlı bir integrali tekrarlı bir integrale indirgemek Çift katlı integralleri hesaplarken, iki durumu ayırt etmek gerekir. () İlk durum. Entegrasyon bölgesi solda sınırlıdır
YÜKSEK İLETİŞİM KOLEJİ T 000 Uzmanlık alanı öğrencileri için "YÜKSEK MATEMATİK" bölüm II disiplininde STANDART HESAPLAMALARIN TOPLANMASI Posta hizmetleri Minsk 00 Ryabenkova LA tarafından derlenmiştir Yayın toplantıda onaylanmıştır.
DERS İkinci dereceden hiperbol çizgileri Örnek olarak, bir daireyi, parabolü, elipsi ve Çemberi tanımlayan denklemler bulacağız. Bir daire, belirli bir düzlemden eşit uzaklıktaki bir düzlem üzerindeki noktaların kümesidir.
Üçlü integral Volchenko Yu.M. Ders içeriği Üç katlı integral kavramı. Varlığının koşulları. Ortalama değer teoremi. Kartezyen ve eğrisel koordinatlarda üçlü integralin hesaplanması. Üçlü
DERS N. Çoklu integrallerin hesaplanması..dikdörtgen Kartezyen koordinatlarda çift katlı integralin hesaplanması.....çift katlı integralin (keyfi bölge) hesaplanması...üçlü integral.....hesaplama
Giriş Kılavuzlar, “Düzlemde ve uzayda düz çizgi”, “Düzlem”, “Eğriler ve ikinci dereceden yüzeyler” konularını içeren 26 bireysel ödev versiyonunu içermektedir. Bireysel olarak
İçindekiler Giriş Çoklu, eğrisel ve yüzey integralleri Alan teorisinin unsurları Sınıf dersleri için problemler Teoriden kısa bilgi Problem çözme örnekleri Kendi kendine hazırlık problemleri Test
Uygulamalı ders 6 Yüzey integralleri 6. Tür yüzey integralinin özelliğinin tanımı, hesaplanması ve uygulamaları 6. Tür yüzey integralinin özelliğinin tanımı ve hesaplanması 6 Tanım
B. M. Mavrin, E. I. Balaev DÖNÜŞ ORGANLARININ GÖRÜNTÜSÜ Çalıştay Samara 2005 FEDERAL EĞİTİM AJANSI DEVLET YÜKSEK MESLEKİ EĞİTİM KURUMU “SAMARSKY”
Çift katlı integraller Bağımsız çalışmaya yönelik problemler ve alıştırmalar 1. Çift katlı f(x, y) dx dy integralini iki şekilde tekrarlı bir integrale azaltın: G a) G, köşeleri (1, 1), (4, 1) olan bir üçgendir ), (4, 4); B)
Federal Demiryolu Taşımacılığı Ajansı Ural Devlet Taşımacılık Üniversitesi Yüksek Matematik Bölümü I N Pirogova Örnekler ve problemlerde analitik geometri Yekaterinburg
Dersler 1-2. Belirli integral ve uygulamaları I. Newton-Leibniz formülünü kullanarak belirli integrali hesaplayın: 1. (2 + 2) 2. / 3. (4.) 5. 6. 7. 8. Efimov-Pospelov 7.324-7.352, 7.380- 7.385,
Ders 7 Uygun olmayan integraller Uygun olmayan integraller, belirli (uygun) bir integralin varoluş koşullarından en az birinin karşılanmadığı belirli integrallerdir :) veya
14. ders. Üç katlı integraller Mat. analiz, uygulama matematik, 3. dönem Revizyon A1 Bir sonraki integralde kutupsal koordinatlara gidin ve integralin limitlerini her iki sıraya göre düzenleyin:
Rusya Federasyonu Eğitim Bakanlığı Yaroslavl Devlet Üniversitesi adını almıştır. P.G. Demidova Ayrık Analiz Bölümü UZAYDA DÜZLEM VE ÇİZGİ Problemleri Yaroslavl Ph.D. tarafından derlenmiştir.
MOSKOVA OTOMOBİL VE KARAYOLLARI DEVLET TEKNİK ÜNİVERSİTESİ (MADI) İNTEGRAL HESABI Test görevlerinin çeşitleri Sorun kitabı MOSKOVA OTOMOBİL VE KARAYOLLARI DEVLET TEKNİK ÜNİVERSİTESİ
Federal Demiryolu Taşımacılığı Ajansı Ural Devlet Taşımacılık Üniversitesi Yüksek ve Uygulamalı Matematik Bölümü P I Gnilomedov ÇOKLU VE EĞRİSEL İNTEGRALLERİN UYGULAMALARI
RUSYA FEDERASYONU EĞİTİM VE BİLİM BAKANLIĞI FEDERAL DEVLET ÖZERK EĞİTİM KURUMU YÜKSEKÖĞRETİM "SAMARA DEVLET HAVACILIK UZAY ÜNİVERSİTESİ"
Ek 5 Rusya Federasyonu Tarım Bakanlığı Federal Devlet Bütçe Yüksek Öğretim Kurumu "Saratov Devlet Tarım Üniversitesi"
DÜZLEMDE ANALİTİK GEOMETRİ ELEMANLARI. Düz çizgi 1. Köşeleri A(6; 7), B(3; 3), C(1; 5) noktaları olan bir üçgenin çevresini hesaplayın. 2. A(7;) noktalarından eşit uzaklıkta bir nokta bulun.
Rusya Federasyonu Eğitim ve Bilim Bakanlığı Yaroslavl Devlet Üniversitesi adını almıştır. P. G. Demidova Cebir ve Matematiksel Mantık Bölümü İkinci Dereceden Eğriler Bölüm I Metodolojik Talimatlar
İçerikler Çoklu integraller Çoklu integral kavramı Çift katlı integraller. Düzlemdeki bölgeler.................. Tekrarlanan integral................. 3.3 Kartezyen koordinatlarda çift katlı integralin hesaplanması.. ..................
Pratik Ders 14 Konu: Parabol Planı 1. Bir parabolün tanımı ve kanonik denklemi. Bir parabolün ve merkezinden geçen bir çizginin göreceli konumu. Temel
1 Bir düzlem üzerinde analitik geometrinin en basit problemleri 11 İki nokta arasındaki mesafe Dikdörtgen bir koordinat sistemi düşünün (Kartezyen, Şekil. 1 Herhangi bir M noktası OA x koordinatlarına karşılık gelir)
RUSYA FEDERASYONU ULAŞTIRMA BAKANLIĞI FEDERAL DEVLET EĞİTİM YÜKSEK MESLEKİ EĞİTİM KURUMU ULYANOVSK YÜKSEK HAVACILIK SİVİL HAVACILIK YÜKSEKOKULU (ENSTİTÜ)
Bölüm 5. Üç katlı integral. 5.1. Üç katlı integralin tanımı. Önceki bölümde çift katlı integral kavramını tanıttıktan sonra, bu kavramın üç boyutlu uzaya daha genellemesini yapmak doğal olacaktır.
DÜZLEMDE CEBİR ÇİZGİLER.. İLK DERECEDEN DOĞRULAR (DÜZLEMDE ÇİZGİLER... DÜZLEMDE DOĞRU DENKLEMLERİNİN TEMEL TÜRLERİ. Belirli bir çizgiye dik sıfır olmayan bir vektör n'ye normal denir
RUSYA FEDERASYONU EĞİTİM VE BİLİM BAKANLIĞI IMGUBKIN TS Filippova ANFILIPOV'UN ADINI ALAN RUSYA DEVLET PETROL VE GAZ ÜNİVERSİTESİ “Çoklu ve eğrisel” konusunu incelemek için METODOLOJİK TALİMATLAR
Penza Devlet Pedagoji Üniversitesi, adını VGBelinsky OGNikitin'den almıştır. ÇEŞİTLİ DEĞİŞKENLERİN FONKSİYONLARI İNTEGRAL HESABI Ders Kitabı Penza Yazı işleri ve yayıncılık departmanının kararı ile yayınlanmıştır.
Konu DÜZLEMDE VE UZAYDA ANALİTİK GEOMETRİ ELEMANLARI Ders anlatımı.. Düzlemde düz çizgiler Plan. Düzlemde koordinat yöntemi.. Kartezyen koordinatlarda düz çizgi.. Paralellik ve diklik durumu
Moskova Devlet Teknik Üniversitesi N.E. Bauman Temel Bilimler Fakültesi Matematiksel Modelleme Bölümü A.N. Kaviakovykov, A.P. Kremenko
Bölüm 5. Tip yüzey integralleri (devamı) 5 Sınıf problemleri Problem 5 (4349) Koni yüzeyinin z d, x = ρ cos ϕ sin α, y = ρ sin ϕ sin α, z = olduğu noktada integrali hesaplayın. ρ çünkü α (( ρh,
Federal Eğitim Ajansı Ural Devlet Ormancılık Üniversitesi Malzeme Mukavemeti ve Teorik Mekanik Bölümü V. A. Kalentyev V. M. Kalinin L. T. Raevskaya N. I. Chashchin
ANALİTİK GEOMETRİ ELEMANLARI ÜÇ BOYUTLU UZAYDA BİR DÜZLEMİN SINIFLANDIRILMASI Bir düzlemin vektör denklemini yazın ve bu denklemin içerdiği niceliklerin anlamını açıklayın Bir düzlemin genel denklemini yazın
3 Örnek Düz bir malzeme bölgesinin (D) statik momentleri için ifadeler yazın (Φ) şeklini hesaba katan formül (3)'e dayanarak, elimizde: ρ, dd, ρ, dd Statik momentin mekanik anlamına dayanarak,
Problem 1 Yarım dairenin ağırlık merkezinin koordinatlarını bulun y = r 2 x 2. Problem 5 x 2 + y 2 = 16 yüzeyinin içinde bulunan z = 1 4 xy yüzeyinin bir kısmının alanı. 2 Entegrasyon sırasını değiştirin
UKRAYNA EĞİTİM VE BİLİM BAKANLIĞI UKRAYNA ULUSAL METALÜRJİ AKADEMİSİ Disiplindeki problemlerin çözümü için METODOLOJİK TALİMATLAR Yüksek Matematik ve pratik test seçenekleri
Yüksek matematik dersinde (III dönem) “Yüksek matematikte bireysel ödevlerin toplanması” ders kitabına dayanan pratik dersler, cilt 3, ed. Ryabushko A.P. tam zamanlı öğrenciler için
Moskova Devlet Teknik Üniversitesi N.E. Bauman Temel Bilimler Fakültesi Hesaplamalı Matematik ve Matematiksel Fizik Bölümü A.I. Levin ÇOKLU İNTEGRALLER Elektronik
Yay uzunluğu (birinci tür) yüzeyi boyunca yüzey alanına (birinci tür) göre çift üçlü eğrisel bir fonksiyonun birkaç değişkenli bir fonksiyonunun integral hesabı f() fonksiyonu tanımlansın
1.3. Ders 3 1.3.1. Kartezyen koordinatlarda üçlü integrallerin hesaplanması Uzaysal bir alan olsun, D onun Oksi düzlemine izdüşümü olsun. Herhangi bir dikey çizgi varsa, bölgeye -düzenli denir
BELARUS CUMHURİYETİ EĞİTİM BAKANLIĞI Belarus Ulusal Teknik Üniversitesi Mühendislik Matematik Bölümü YÜKSEK MATEMATİK Mekanik ve teknolojik öğrenciler için problem çözme kılavuzu
Pratik ders 1 Konu: Hiperbol Planı 1 Bir hiperbolün tanımı ve kanonik denklemi Bir hiperbolün geometrik özellikleri Bir hiperbolün ve merkezinden geçen bir çizginin göreli konumu Asimptotlar
kesinlikle
.
İzin vermek 
,
.
Bir kümeye kapalı aralık veya kapalı çubuk denir. 
.
kümesine açık aralık denir
veya açık bir ışın 
.
kesinlikle
.
Aralıkların ölçüsü 
Ve 
miktar denir:
(Daha doğrusu 
).
kesinlikle
.
Eğer 
Öyle ki 
o zaman aralık 
dejenere denir ve 
.
Boşluk ölçüsünün özellikleri:
A). Pozitiflik: 
, Ve 
o zaman ve yalnızca ne zaman 
– dejenere.
B). Pozitif homojenlik: .
V). Toplanabilirlik:
* İçin 
Öyle ki 
;
* İçin 
Ve 
.
G). Ölçünün monotonluğu: .
kesinlikle . Kirişin çapı (boşluk) şu değerdir:
Dikkat 
Ve 
– bu aynı şey değil. Örneğin, eğer
– dejenere o zaman 
,A 
(genel olarak konuşursak).
Bu durumda: * ;
*
;*
.
kesinlikle
.
Bütünlük 
aralığın alt açıklıkları 
aralık bölümü denir 
, Eğer: *;
*
;
*
;
*
;
*
.
Büyüklük 
bölüm parametresi denir P(aynı zamanda 
).
kesinlikle
.
Bölme 
bölüm iyileştirme denir 
, eğer bölümün tüm öğeleri 
bölüm elemanlarının bölümlenmesiyle elde edilir 
.
Şununla belirtilir: 
. Okumak: 
daha küçük 
veya 
daha büyük 
.
“Daha büyük – daha küçük” oranı için aşağıdakiler doğrudur:
*. geçişlilik – ; 
;
*.
;
*.
|
.
*.
§. Çoklu integralin tanımı 
İzin vermek 
,
– kereste (boşluk) – boşluğu bölmek BEN 
. Bölümün her aralığında 
.
noktayı işaretle 
Aldık 
.
Büyüklük 
için işaretli noktalara sahip bölüm fonksiyonun Riemann integral toplamı denir
(F X – boşluğu bölmek
) aralıkta 
.
kesinlikle
:
=
=
.
işaretli noktalarla bölümlere göre 
Belirleme – boşluğu bölmek
– kirişe entegre edilmiş birçok fonksiyon
kesinlikle
:
ε
> 0 
δ>0<
.
hadi yazalım: fonksiyonun Riemann integral toplamı denir(F Eğer fonksiyon için – boşluğu bölmek) Açık 
ve bölümler 
- ile belirtmek fonksiyonun Riemann integral toplamı denir(F Eğer fonksiyon için – boşluğu bölmek – fonksiyonun en büyük ve en küçük değeri k 
=
Ve 
=
daha sonra değerler
§. alt ve üst Darboux toplamları denir..
Çoklu integralin varlığı için Darboux kriteri 0
.
T 
İşlevsel olmak 
kirişe entegre edildi 
(onlar. 
.
Δ▲.
) gerekli ve yeterlidir, böylece
Öklid uzayında bir fonksiyonun bir kiriş üzerindeki entegrasyonu tanımlanır. Bir fonksiyon Öklid uzayından keyfi olarak sınırlanmış bir küme üzerinden nasıl entegre edilebilir? fonksiyonun Riemann integral toplamı denir
Fonksiyonun integralini tanımlayalım
.
kesinlikle
:
birçok kişi tarafından 
Ve 
İzin vermek 
– sınırlı, yani 
. İşlev.
kümenin karakteristik fonksiyonu diyoruz 
≡
.
M Daha sonra: Küme integralinin tanımı hangi ışının içerdiğine bağlı değildir. 
.
M
seçilmiş, yani Bu, bir küme üzerindeki integralin tanımının doğru olduğu anlamına gelir. fonksiyonun Riemann integral toplamı denir(F Eğer fonksiyon için Daha sonra:İntegrallenebilirlik için gerekli bir koşul. fonksiyonun Riemann integral toplamı denir(Fİşlevsel olmak Daha sonra:. Δ▲.
entegre edilebilir olması gereklidir
1 . ) ile sınırlıydı §. Çoklu integrallerin özellikleri. İşlev Doğrusallık: Çok R bir sette entegre edilebilir fonksiyonlar
M - 
doğrusal
2
.
uzay ve 
– doğrusal fonksiyonel. 
Normalleştirme koşulu:
3 . . Başka bir giriş şekli
esasen Öklid uzayından keyfi bir kümenin ölçüsünü belirler.
Bir Lebesgue ölçüsü sıfır kümesi üzerinde bir integral mevcutsa, o zaman sıfıra eşittir. Daha sonra: Not:
Birçok 
Lebesgue ölçüsü sıfır kümesi denir, 
Ve 
.
4 . Eğer;Öyle ki;
A. B. 
Ve 
V. Daha sonra: Eğer 
5
.
Ve fonksiyonun Riemann integral toplamı denir=– sıfırdan ayrılmış, O Daha sonra: Eğer 
.
6
.
G 
Ve 
p.v. (neredeyse her yerde) açık
,
Toplanabilirlik: Eğer 
.
O
7
.
Genel olarak: 
Ve 
p.v. (neredeyse her yerde) açık 
.
8
.
Δ. Eşitlikten şu sonuç çıkar: ▲ 
Monoton:
.
9
.
birçok kişi tarafından 
Eşitsizliklerin entegrasyonu: eğer 
ito Daha sonra:. İçin fonksiyonun Riemann integral toplamı denir
(F, kümenin bir iç noktasının olması gerekli ve yeterlidir
10
.
Entegre edilebilir fonksiyon modülünün entegre edilebilirliği: 
.
11
.
Ortalama değer teoremi: 
,
Açık Daha sonra: işareti korur ve 
, O
.
Eğer set Daha sonra:– tutarlı ve fonksiyonun Riemann integral toplamı denir(F) – sürekli açık 
p.v. (neredeyse her yerde) açık 
Öyle ki 
.
12 . Negatif olmayan bir fonksiyonun integralinin 0'a eşit olması için
için gerekli ve yeterli fonksiyonun Riemann integral toplamı denir(F) = 0 neredeyse her yerde Daha sonra:.
13 . Fubini teoremi.Çift katlı integral için:
Bırakın alan 
- dikdörtgen:. Daha sonra, iç tek integrallerin mevcut olması koşuluyla, çift katlı integrali bulmak için tekrarlı integrale geçebilirsiniz (bkz. Şekil a):
, veya
e
.
(*)
Bir Lebesgue ölçüsü sıfır kümesi üzerinde bir integral mevcutsa, o zaman Entegrasyonun dış sınırları sabit olmalıdır; entegrasyonun iç sınırları, henüz entegrasyonun gerçekleştirileceği değişkene bağlı olabilir.
Formül (*), karakteristik ayarlama fonksiyonu kullanılarak elde edilebilir D.
Çoklu integral için:
Let ve Öklid uzaylarının bazı alt kümeleri 
Ve 
. Öklid uzayının bir alt kümesi olan bu kümelerin Kartezyen çarpımını tanımlayalım. 
:.
O zaman Fubini teoremi 
şu forma sahiptir: 
.
Teorem kirişler için de geçerlidir X Ve e ve daha karmaşık konfigürasyonlar için.
Örnekler:
1
0
.
Hesaplamak 
, eğer alanın sınırı 
denklemlerle verilir:
. 
Ve 
Alanın sınırını belirleyen eğrilerin kesişme noktalarını bularak iki nokta elde ederiz:. Daha sonra yinelenen integrallere geçerken olası entegrasyon limitleri düzenlemesi şunu verir: 
;
2
.
–
.
Yinelenen integraldeki entegrasyon sırasını değiştirin: Yemek tarifi:
3
Hesaplamak:
, Eğer 
.
Yinelenen integrallere geçmek şunları sağlar: Aynı zamanda üçlü integralde limitlerin yerleştirilmesi integralin iç limitleriyle başlamalıdır. Daha sonra alanı projelendirin V uçağa
xOy D alanda sınırlar koymak uçağa.
4
0
.
– uçakta yatmak 
.
Yinelenen integraldeki entegrasyon sırasını değiştirin: Çoklu integral Düzlemdeki bir alanda tanımlanan bir fonksiyonun üç boyutlu integrali veya N Düzlemdeki bir alanda tanımlanan bir fonksiyonun üç boyutlu integrali veya boyutlu uzay. K. ve. çift katlı integraller, üç katlı integraller vb. arasındaki farkı ayırt edin. -çoklu integraller. fonksiyonun Riemann integral toplamı denir(Fonksiyona izin ver x, y D) bazı bölgelerde verilir uçak xOy. D Alanı bölelim Düzlemdeki bir alanda tanımlanan bir fonksiyonun üç boyutlu integrali veya Açık kısmi alanlar ben, alanları eşit olan ben mi her alanda seçim yapın ben mi nokta (, ξiηi ) (santimetre.
pirinç. ) ve integral toplamını oluşturun her alanda seçim yapın Kısmi alanların maksimum çapında sınırsız bir azalma varsa miktarlar S nokta (, ξi noktaların seçiminden bağımsız olarak bir sınırı vardır ( fonksiyonun Riemann integral toplamı denir(x, y) bölgeye göre D ve belirtmek Üç katlı integral benzer şekilde tanımlanır ve genel olarak, Düzlemdeki bir alanda tanımlanan bir fonksiyonun üç boyutlu integrali veya-çoklu integral. Çift katlı bir integralin varlığı için örneğin bölgenin olması yeterlidir. D kapalı karelenebilir bir bölgeydi (Bkz. Karelenebilir bölge) ve fonksiyon fonksiyonun Riemann integral toplamı denir(Fonksiyona izin ver) sürekliydi D. K. ve. basit İntegrallerin özelliklerine benzer bir dizi özelliğe sahiptir .
K.'yi hesaplamak için ve. genellikle onu yinelenen bir integrale götürür (bkz. Yinelenen integral). K.'nın bilgisi için özel durumlarda ve. Green formülü ve Ostrogradsky formülü daha düşük boyutlu integraller olarak hizmet edebilir. K. ve. Kapsamlı uygulamalara sahiptir: cisimlerin hacimlerini, kütlelerini, statik momentlerini, eylemsizlik momentlerini vb. ifade etmek için kullanılırlar.
Büyük Sovyet Ansiklopedisi. - M .: Sovyet Ansiklopedisi. 1969-1978 .
Diğer sözlüklerde “Çoklu integralin” ne olduğuna bakın:
Çok değişkenli bir fonksiyonun integrali. Tek değişkenli bir fonksiyonun belirli integraline benzer şekilde integral toplamları kullanılarak belirlenir (bkz. İntegral hesabı). Değişken sayısına bağlı olarak ikili, üçlü, n... ... Büyük Ansiklopedik Sözlük
Çok değişkenli bir fonksiyonun belirli integrali. K. ve'nin çeşitli kavramları vardır. (Riemann integrali, Lebesgue integrali, Lebesgue Stieltjes integrali, vb.). Çoklu Riemann integrali Jordan ölçüsüne dayalı olarak tanıtılmıştır. E, Jordan'la ölçülebilir olsun... ... Matematik Ansiklopedisi
Matematiksel analizde çoklu veya çoklu integral, değişkenlerden alınan bir dizi integraldir. Örneğin: Not: Çoklu bir integral belirli bir integraldir; hesaplaması her zaman bir sayıyla sonuçlanır. İçindekiler 1... ...Wikipedia
Çok değişkenli bir fonksiyonun integrali. Tek değişkenli bir fonksiyonun belirli integraline benzer şekilde integral toplamları kullanılarak belirlenir (bkz. İntegral hesabı). Değişken sayısına bağlı olarak ikili, üçlü, n... ... Ansiklopedik Sözlük
Çok değişkenli bir fonksiyonun integrali. Benzer şekilde tanımlanan integral toplamlar kullanılarak belirlenir. tek değişkenli bir fonksiyonun integrali (bkz. İntegral hesabı). Değişken sayısına bağlı olarak ikili, üçlü, i... ... Doğa bilimi. Ansiklopedik Sözlük
Not: Bu makalede işaretin kullanıldığı her yerde, aksi belirtilmedikçe (çoklu) Riemann integrali kastedilmektedir; Bir kümenin ölçülebilirliğinden bahsettiğimiz bu makalenin her yerinde, Ürdün ölçülebilirliğini kastediyoruz, değilse de... ... Vikipedi
Bir trigonometrik toplamın modülünün 2k derecesinin ortalama değeri olan formun çoklu integrali. Vinogradov'un bu integralin değerine ilişkin teoremi, ortalama değer teoremi, Weyl toplamlarının tahminlerinin temelini oluşturur. Edebiyat Vinogradova int... Vikipedi
Bir şeklin alanı olarak belirli integral Bu terimin başka anlamları da vardır, bkz. İntegral (anlamlar). Bir fonksiyonun integrali ... Vikipedi
Farklı değişkenler üzerinde entegrasyonun sırayla gerçekleştirildiği bir integral, yani (1) formunun bir integrali. f(x, y) fonksiyonu, X ve Y uzaylarının XX Y direkt çarpımında bulunan A kümesi üzerinde tanımlanır, burada s'ye mx ve my sonlu ölçüler verilmiştir,… … Matematik Ansiklopedisi
Bir düzlemdeki veya uzaydaki herhangi bir eğri boyunca alınan bir integral. K. ve. 1. ve 2. tip. K. ve. Tip 1, örneğin değişken yoğunluk eğrisinin kütlesinin hesaplanması problemi ele alındığında ortaya çıkar; belirlenmiş... ... Büyük Sovyet Ansiklopedisi
Ostrogradsky'nin çoklu integraller üzerindeki çalışması üzerinde biraz ayrıntılı olarak duralım.
Ostrogradsky'nin üçlü integrali çift integrale dönüştürme formülü, genellikle şu şekilde yazıyoruz:
burada div A, A vektörünün alanının diverjansıdır,
Аn, A vektörünün ve sınır yüzeyinin dış normali n'nin birim vektörünün skaler çarpımıdır; matematik literatüründe daha önce genellikle Gauss ve Green adlarıyla ilişkilendirilirdi.
Aslında, Gauss'un küresellerin çekiciliği üzerine çalışmasında, formül (1)'in yalnızca çok özel durumları görülebilir; örneğin P = x, Q = R = 0, vb. J. Green'e gelince, onun çalışmasında elektrik teorisine göre ve formül (1)'de hiç manyetizma yoktur; üçlü ve çift katlı integraller arasında başka bir ilişki türetir, yani Green'in Laplace operatörü için formülü şu şekilde yazılabilir:
Elbette, formül (1)'i (2)'den türetebiliriz.
ve aynı şekilde formül (1)'den formül (2)'yi elde etmek mümkündür, ancak Green bunu yapmayı düşünmemiştir.
solda hacim üzerindeki integral, sağda sınır yüzeyi üzerindeki integral ve bunlar dış normalin yön kosinüsleridir.
Ostrogradsky'nin Paris el yazmaları, integral teoreminin (1) hem keşfinin hem de ilk mesajının kendisine ait olduğunu tam bir kesinlikle kanıtlıyor. İlk kez, tam da şimdi yaptıkları gibi, 13 Şubat 1826'da Paris Bilimler Akademisi'ne sunulan "İntegral Hesap Teoreminin Kanıtı"nda ifade edilmiş ve kanıtlanmıştır. Ostrogradsky'nin 6 Ağustos 1827'de sunduğu "Katılarda Isı Difüzyonu Üzerine Anı". "Anı" inceleme için Fourier ve Poisson'a verildi ve ikincisi, ilkindeki girişten de anlaşılacağı üzere kesinlikle okudu. el yazmasının her iki bölümünün sayfaları. Elbette, esneklik teorisi üzerine çalışmasını sunmadan iki yıl önce Ostrogradsky'nin çalışmasında tanıdığı teoremi kendisine atfetme fikri Poisson'un aklına bile gelmedi.
Ostrogradsky ve Green'in çoklu integralleri üzerine yaptıkları çalışmalar arasındaki ilişkiye gelince, “Isı Teorisi Üzerine Not”ta Green'in kendi formülünü çok özel bir durum olarak kapsayan bir formülün türetildiğini hatırlıyoruz. Ostrogradsky'nin "Not"ta kullandığı artık alışılmadık Cauchy sembolizmi, yakın zamana kadar bu önemli keşfi araştırmacılardan gizledi. Elbette Greene, Laplace operatörleri için kendi adını taşıyan formülü keşfetmenin ve 1828'de ilk kez yayınlamanın onurunu koruyor.
Üç katlı bir integrali çift katlı bir integrale dönüştürmek için bir formülün keşfi, Ostrogradsky'nin bir n-katlı integrali değiştirme problemini çözmesine, yani integrali bir n-'ye göre diverjans tipinin bir ifadesinden dönüştürmeye yönelik genel formülü türetmesine yardımcı oldu. boyutsal alan ve onu L(x,y, z,…)=0 denklemiyle sınırlayan süper yüzey S üzerindeki integral. Önceki gösterime sadık kalırsak, formül şu şekildedir:
Ancak Ostrogradsky bizim kullandığımız geometrik görüntüleri ve terimleri kullanmadı: çok boyutlu uzayların geometrisi o zamanlar henüz mevcut değildi.
“Çoklu İntegrallerin Değişimleri Hesabı Üzerine Anı”da bu tür integrallerin teorisindeki iki önemli konu daha ele alınmaktadır. İlk olarak Ostrogradsky, çok boyutlu bir integraldeki değişkenleri değiştirmek için bir formül türetiyor; ikinci olarak, ilk kez, uygun limitler dahilinde değişkenlerin her biri üzerinde n ardışık entegrasyon kullanarak n katlı bir integrali hesaplama yönteminin tam ve doğru bir tanımını veriyor. Son olarak, bu anıda yer alan formüllerden, çok boyutlu bir integralin parametresine göre türev almanın genel kuralı, yalnızca integral fonksiyonu değil aynı zamanda integral alanının sınırı da bu parametreye bağlı olduğunda kolayca türetilir. Adı geçen kural, anılardaki formüllerden o kadar doğal bir şekilde çıkıyor ki, daha sonraki matematikçiler onu bu anıdaki formüllerden biriyle bile özdeşleştirdiler.
Ostrogradsky, çoklu integrallerdeki değişkenleri değiştirmeye özel bir çalışma ayırdı. Çift katlı integral için karşılık gelen kural, Euler tarafından üçlü integral - Lagrange için biçimsel dönüşümler kullanılarak türetildi. Ancak Lagrange'ın sonucu doğru olsa da muhakemesi doğru değildi: Eski ve yeni değişkenlerdeki (koordinatlar) hacim elemanlarının birbirine eşit olduğu gerçeğinden yola çıkıyor gibiydi. Ostrogradsky, başlangıçta, değişkenlerin yerini değiştirme kuralının az önce bahsedilen türetilmesinde benzer bir hata yaptı. Ostrogradsky, "Çoklu integrallerdeki değişkenlerin dönüşümü üzerine" makalesinde Lagrange'ın hatasını ortaya çıkardı ve ayrıca ilk kez değişkenleri çift katlı bir integrale dönüştürmek için görsel geometrik yöntemin de biraz daha titiz bir biçimde sunulduğunu açıkladı. kılavuzlarımızda. Yani, formüller kullanılarak integraldeki değişkenler değiştirilirken, entegrasyon alanı u=const, v=const iki sistemin koordinat çizgileriyle sonsuz küçük eğrisel dörtgenlere bölünür. Daha sonra integral, önce sonsuz dar kavisli bir şeride karşılık gelen elemanların toplanmasıyla ve ardından hepsi tükenene kadar elemanların şeritler halinde toplanmasına devam edilerek elde edilebilir. Basit bir hesaplama, en küçük yüksek mertebeden olanlara kadar paralelkenar olarak kabul edilebilecek alan için, alanın pozitif olacak şekilde seçildiği ifadeyi verir. Sonuç, iyi bilinen formüldür
Olarak belirtilen iki değişkenli bir fonksiyon için z = fonksiyonun Riemann integral toplamı denir(F, sen) .
Çift katlı integral şu şekilde yazılır:
Burada D– çift katlı integralin hesaplanması görevinde ifadeleri (eşitlikler) verilen, çizgilerle sınırlanmış düz bir şekil. Sol ve sağ, soldaki değişkenin olduğu eşitliklerdir F, ve üstü ve altı – soldaki değişkenin olduğu eşitliklere göre sen. Burası çift katlı integral hesaplama tekniğinin anlaşılması için en önemli yerlerden biri olmaya devam ediyor.
Çift katlı integrali hesaplayın - belirtilen şeklin alanına eşit bir sayı bulmak anlamına gelir D .
Biz dokunana kadar çift katlı integral tanımları ve bunu hesaplamayı öğreneceğiz. Çift katlı integralin ne olduğunu anlamak, onu hesaplamak için birkaç problem çözdüğünüzde daha kolaydır; dolayısıyla çift katlı integralin tanımını bu dersin sonunda bulacaksınız. Biraz ileriye baktığımızda, çift katlı integralin tanımının da söz konusu şekil ile ilgili olduğunu söyleyebiliriz. D .
Şekil ise D bir dikdörtgendir ve onu çevreleyen tüm çizgiler düz çizgilerdir. Şekil ise D- eğriseldir, daha sonra solda ve sağda düz çizgilerle ve üstünde ve altında görevde verilen eşitliklerle verilen kavisli çizgilerle sınırlıdır. Bir figürün olduğu durumlar da vardır. D- bir üçgen, ancak bu gibi durumlarda daha fazlası biraz daha ileride.
Bu nedenle çift katlı integrali hesaplamak için şekli çevreleyen çizgileri sıralamak gerekir. D Kesin bir adı olan entegrasyon bölgesi. Sol ve sağ, üst ve alt olarak sıralayın. Bu, aşağıdaki durumlarda gerekli olacaktır: bir çift katlı integralin yinelenen bir integrale indirgenmesi – çift katlı integrali hesaplama yöntemi.
Dikdörtgen alan durumu:
Eğri bir bölge durumu:
Ve bu zaten, entegrasyonun üst ve alt sınırlarının verildiği bilinen belirli integrallerin bir çözümüdür. Bir şekli sınırlayan çizgileri tanımlayan ifadeler D, halihazırda yaklaşmakta olduğumuz olağan belirli integrallerin integral limitleri olacaktır.
Çift katlı bir integralin tekrarlanan bir integrale indirgenmesi
Dikdörtgen bölge durumu
Böyle bir fonksiyonun çift katlı integrali olsun
İle bu çift katlı integrali değerlendirin , onu yinelenen bir integrale indirgememiz gerekiyor, bu da şu forma sahip:
.
Öncelikle iç (sağ) belirli integrali, ardından dış (sol) belirli integrali hesaplamanız gerekir.
Rolleri değiştirebilirsiniz F Ve sen
.
Örnek 1.Çift katlı integrali hesaplayın
Y'yi bir sabit olarak kabul ederek iç (sağ) integrali hesaplıyoruz. Anladık.
.
Örnek 2.Çift katlı integrali hesaplayın
,
Çözüm. Bu çift katlı integrali yinelenen bir integrale indirgeyelim
Çizimde entegrasyon bölgesini oluşturuyoruz:
Şimdi az önce hesaplanan iç kısmın (sağ) dış (sol) integralini hesaplıyoruz:
Sonuç bu çift katlı integralin çözümü olacaktır.
Çift katlı integrali kendiniz hesaplayın ve sonra çözüme bakın
Kavisli veya üçgen bölge durumu
Bize yine iki değişkenli bir fonksiyon verilsin fonksiyonun Riemann integral toplamı denir(F, sen) ve kısıtlamalar D: zaten biraz farklı bir türde:
Bu giriş, şeklin anlamına gelir D doğrusal bir bölgede olduğu gibi sol ve sağ sınırlıdır - düz çizgiler F = A Ve F = B, ancak altında ve üstünde denklemler tarafından verilen eğriler vardır ve . Başka bir deyişle ve fonksiyonlardır.
Böyle bir fonksiyonun çift katlı integrali olsun
Bu çift katlı integrali değerlendirmek için onu yinelenen bir integrale indirgememiz gerekir;
.
İşte entegrasyonun sınırları A Ve B- sayılar ve ve - işlevler. Üçgensel bir bölge durumunda fonksiyonlardan biri düz bir çizginin denklemidir. Bu durum Örnek 3'te tartışılacaktır.
Doğrusal bir bölgede olduğu gibi, önce sağdaki belirli integrali, ardından soldaki belirli integrali hesaplamanız gerekir.
Aynı şekilde rolleri değiştirebilirsiniz F Ve sen. O zaman tekrarlanan integral şu şekle sahip olacaktır:
.
Böyle tekrarlanan bir integral tamamen aynı şekilde çözülmelidir: önce - iç (sağ) integral, sonra - dış (sol).
Örnek 5.Çift katlı integrali hesaplayın
,
Çözüm. Bu çift katlı integrali yinelenen bir integrale indirgeyelim
.
Çizimde entegrasyon bölgesini oluşturuyoruz ve bunun üçgen olduğunu görüyoruz:
X'in bir sabit olduğunu düşünerek iç (sağ) integrali hesaplıyoruz. Anladık.
Şimdi az önce hesaplanan iç kısmın (sağ) dış (sol) integralini hesaplıyoruz. Öncelikle bu integrali integrallerin toplamı olarak sunuyoruz:
.
İlk terimi hesaplıyoruz:
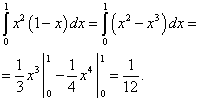
İkinci terimi hesaplıyoruz:
Üçüncü terimi hesaplıyoruz:
Bu çift katlı integralin çözümü olacak toplamı elde ederiz:
.
Örnek 6.Çift katlı integrali hesaplayın
Çözüm. Bu çift katlı integrali yinelenen bir integrale indirgeyelim
Çizimde entegrasyon bölgesini oluşturuyoruz:
X'in bir sabit olduğunu düşünerek iç (sağ) integrali hesaplıyoruz. Anladık.
.
Şimdi az önce hesaplanan iç kısmın (sağ) dış (sol) integralini hesaplıyoruz:
Sonuç bu çift katlı integralin çözümü olacaktır.
F-doğru ve yanlış sen-doğru ve yanlış entegrasyon alanları
Bir çift katlı integralin integral alanı öyle çizgilerle sınırlıdır ki, integral alanını parçalara bölmek ve karşılık gelen her tekrarlanan integrali ayrı ayrı çözmek gerekli hale gelir. Bunlar aşağıdaki durumlarda geçerlidir:
1) entegrasyon alanı, alt veya üst (sol veya sağ) sınır şeklinde iki veya daha fazla düz veya kavisli çizgiye sahip bir şekildir;
2) İntegrasyon bölgesi, sınırları çizgilerin ikiden fazla noktada kesiştiği bir şekildir.
Yukarıdakilerin entegrasyon alanının sol veya sağ sınırı için geçerli olması durumunda, yani çizgilerle ifade edilen kısıtlamalar F, daha sonra entegrasyon alanı denir F-yanlış. Eğer çizgi sen = sen0 karşılık gelen sınırla yalnızca bir noktada kesişir ve sınır yalnızca bir düz çizgi veya eğri ise, o zaman entegrasyon alanı denir. F-doğru
Benzer şekilde, çizgilerle tanımlanan sınır şu şekilde ifade edilirse: sen, dümdüz F = F0 birden fazla noktada kesişiyorsa ya da sınır birden fazla düz çizgi ya da eğriden oluşuyorsa integralin tanım bölgesi denir. sen-yanlış. Şimdi işaretleri göster sen- muhtemelen doğru alan oldukça basittir.
Şu ana kadar örneklere baktık F-yanlış ve sen-doğru entegrasyon alanları. Şimdi doğruluk koşulunun ihlal edildiği durumları düşünün.
Örnek 7.İntegral alanı çizgilerle sınırlı olan bir çift katlı integrali hesaplayın sen = F , xy = 1 , sen = 2 .
Çözüm. Entegrasyon alanı sen-yanlış, çünkü alt sınırı tek bir çizgiyle belirtilemez sen = sen(F) . Yukarıdaki şekilde görüldüğü gibi alt sınır aşağıdakilerden oluşur: sen = F(koyu bordo) ve xy= 1 (yeşil). Bu nedenle doğrudan F= 1 (siyah), entegrasyon alanını iki parçaya bölebiliriz - ve .
Bu çift katlı integral şu şekilde hesaplanır:
Entegrasyon sırasını değiştirme
Yukarıda belirtildiği gibi, çift katlı integrali yinelenen bir integrale indirgedikten sonra değişkenleri değiştirebilirsiniz. F Ve sen rolleri değiştirir veya başka bir deyişle entegrasyonun sırasını değiştirir.
Entegrasyon sırasındaki değişiklik mecazi olarak O'Henry'nin şu sözleriyle açıklanabilir: "Bir orman sakini - bir hayvan - kafese girdiğinde bu şekilde davranır ve kafesteki bir sakin - bir insan - bu şekilde davranır - şüphe ormanında kaybolduğunda öyle davranır." O'Henry'ye göre sonuç aynı ve aynı: "Chalmers mektubu bin küçük parçaya böldü ve pahalı halısını yırtmaya başladı, geri dönüp yürüdü ve bunun üzerine ileri." ( O'Henry. Madison Meydanı'ndan Şehrazat.)
O zaman değişkenin sol integrali F ve doğru olanı - tarafından sen, entegrasyon sırasını değiştirdikten sonra her şey tam tersi olacaktır. Daha sonra "yeni" oyun için entegrasyon sınırları "eski" X'ten "ödünç alınmalı" ve "yeni" X için entegrasyon sınırları şu şekilde elde edilmelidir: ters fonksiyon y'nin limitini belirleyen denklemi x için çözüyoruz.
Örnek 8.
.
Çözüm. İntegral sırası değiştirildikten sonra, y üzerindeki integral solak, x üzerindeki integral ise sağ yönlü olacaktır. "Yeni" oyun için entegrasyon limitlerini "eski" X'ten ödünç alacağız, yani alt limit sıfıra, üst limit ise bire eşittir. “Eski” oyun için entegrasyon sınırları denklemler ve ile verilmektedir. Bu denklemleri x için çözdükten sonra x için yeni entegrasyon limitleri elde ederiz:
(alt) ve (üst).
Böylece integralin sırası değiştirildikten sonra tekrarlanan integral şu şekilde yazılacaktır:
.
Çift katlı bir integralde integralin sırası değiştirildikten sonra, integralin alanı genellikle şuna dönüşür: sen-yanlış veya F-yanlış (önceki paragrafa bakınız). Daha sonra entegrasyon alanını parçalara ayırmanız ve karşılık gelen her bir yinelenen integrali ayrı ayrı çözmeniz gerekir.
İntegral alanını parçalara ayırmak birçok öğrenci için bazı zorluklar oluşturduğundan, kendimizi bir önceki paragrafta verilen örnekle sınırlamayacağız, birkaç örneğe daha bakacağız.
Örnek 9. Yinelenen integral için entegrasyon sırasını değiştirin
.
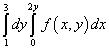Çözüm. Yani bu yinelenen integralin integral alanı düz çizgilerle sınırlıdır sen = 1 , sen = 3 , F = 0 , F = 2sen .
Farklı bir düzende entegrasyon yapıldığında bölgenin alt sınırı iki düz çizgiden oluşur: AB Ve M.Ö. denklemlerle verilen sen= 1 ve sen = F/2, aşağıdaki şekilde görüldüğü gibi.
Bu belirsizlikten kurtulmanın yolu entegrasyon alanını iki parçaya ayırmaktır. Entegrasyon alanının bölümü düz bir çizgi olacaktır BM. Ters fonksiyonu bularak yeni entegrasyon limitlerini hesaplıyoruz. Bu çözüme göre integralin sırası değiştirildikten sonra tekrarlanan integral iki integralin toplamına eşit olacaktır:
Doğal olarak, bu örnekte verilen tekrarlanan integrale indirgenen çift katlı integralin çözümü de aynı olacaktır.
Örnek 10. Yinelenen integral için entegrasyon sırasını değiştirin
.
Çözüm. Dolayısıyla yinelenen integralin integral alanı düz çizgilerle sınırlıdır F = 0 , F= 2 ve eğriler ve .
Aşağıdaki şekilde görüldüğü gibi eksene paralel bir doğru 0x, entegrasyon alanının alt sınırını ikiden fazla noktada kesecektir.
Bu nedenle entegrasyon alanını şekilde siyahla çizilen düz çizgilerle üç parçaya bölüyoruz. Ters fonksiyonu bularak yeni entegrasyon limitlerini hesaplıyoruz. Üç yeni entegrasyon alanının sınırları aşağıdaki gibi olacaktır.
Bu çözüme göre integralin sırası değiştirildikten sonra tekrarlanan integral üç integralin toplamına eşit olacaktır:
Üç integralin aynı toplamı, bu örnekte verilen tekrarlanan integrale indirgenen çift katlı integrale eşit olacaktır.
Ancak yine de mücbir sebepler, öğrencilerin zaten bir önceki adımda olmalarına engel oluyor ve entegrasyonun sınırlarını belirliyor. Kaygı ve kafa karışıklığının bazı temelleri var: İntegral bölgesini parçalara bölmek için genellikle çizime yakından bakmak ve tekrarlanan integrali (integral tablosu) çözmek yeterliyse, o zaman sınırları belirleme konusunda biraz eğitim deneyimine ihtiyaç vardır. entegrasyon. Yalnızca entegrasyonun sınırlarını belirlemeye odaklanacağımız ve - neredeyse otomatik olarak - bölgeyi bölümlemeye ve çözümün kendisini atlamaya odaklanacağımız bir örnek üzerinden gidelim.
Örnek 11.İntegral tanım kümesi ise çift katlı integralin integral limitlerini bulun Dşu şekilde verilmiştir:
sen - 2F ≤ 0;
2 yıl - F ≥ 0;
xy ≤ 2.
Çözüm. Açıkça (üzerinden F Ve sen"safsızlıklar olmadan") entegrasyon bölgesini sınırlayan çizgiler belirtilmemiştir. X için çoğunlukla düz çizgiler olduklarından, bir noktada i ile ifade edilen üst ve alt sınırlara dokunduklarından, o zaman tam olarak bu yol boyunca ilerleyeceğiz. Üstelik entegrasyon sırasını değiştirdiğimizde aynı alana sahip bir entegrasyon bölgesi elde edeceğiz. Oyundaki eşitsizlikleri çözelim ve şunu elde edelim:
sen ≤ 2F;
sen ≥ F/2;
sen ≤ 2/F.
Ortaya çıkan çizgileri çizime göre oluşturuyoruz. X üzerinden integralin sınırları aslında çizgilerdir F= 0 ve F= 2. Ancak entegrasyon alanı ortaya çıktı sen-yanlış, çünkü üst sınırı tek satırla belirtilemez sen = sen(F) .