การบรรยาย: อินทิกรัลหลายตัว, อินทิกรัลคู่ อินทิกรัลหลายตัว ความหมายของอินทิกรัลหลายตัว

การถอดเสียง

1 หน่วยงานของรัฐบาลกลางเพื่อการศึกษา สถาบันการศึกษาของรัฐของการศึกษาวิชาชีพชั้นสูง “มหาวิทยาลัย SAMARA STATE AEROSPACE ตั้งชื่อตามนักวิชาการ SP KOROLEVA” งานและแบบฝึกหัดรวมหลายรายการ ได้รับการอนุมัติโดยสภาบรรณาธิการและสำนักพิมพ์ของมหาวิทยาลัยตามคำแนะนำด้านระเบียบวิธี S A M A R A Publishing House SSAU

2 UDC 7 7 รวบรวมโดย OM Karpilova ผู้ตรวจสอบผู้สมัครรองศาสตราจารย์ GN Gutman ปัญหาปริพันธ์และแบบฝึกหัดหลายประการ: วิธีการบ่งชี้ / องค์ประกอบ OM Karpilova Samara: สำนักพิมพ์ Samara State Aerospace University คอลเลกชันประกอบด้วยตัวอย่างวิธีแก้ไขปัญหาทั่วไปตามหัวข้อ: ปริพันธ์คู่ การประยุกต์ใช้ปริพันธ์สามตัวของปริพันธ์หลายตัว ในแต่ละหัวข้อจะมีการหารือเกี่ยวกับปัญหาทั่วไป วิธีในการแก้ปัญหาจะได้รับการวิเคราะห์อย่างละเอียด และเสนอปัญหาสำหรับงานอิสระ ภาคผนวกมีตัวเลือกสำหรับการบ้านส่วนบุคคล การบ้านทั้งหมดจะถูกรวบรวมตามโปรแกรม สำหรับหลักสูตรคณิตศาสตร์สำหรับนักศึกษามหาวิทยาลัยเทคนิคคำแนะนำด้านระเบียบวิธีที่จัดทำขึ้นที่ภาควิชาวิศวกรรมทั่วไปและมีไว้สำหรับนักศึกษาของสถาบันพลังงานและการขนส่งของมหาวิทยาลัยการบินและอวกาศแห่งรัฐซามารา UDC 7 7 มหาวิทยาลัยการบินและอวกาศแห่งรัฐซามารา

3 การคำนวณจำนวนเต็มคู่ในพิกัดคาร์ทีเซียน ในการคำนวณอินทิกรัลคู่ มันถูกนำเสนอในรูปแบบของอินทิกรัลคู่ที่ซ้ำกัน f f คำตอบของตัวอย่าง ตัวอย่าง ไปจาก b a f ไปยังอินทิกรัลซ้ำ และกำหนดขีดจำกัดของอินทิกรัลหากพื้นที่ถูกจำกัดโดย เส้น: 6; ข; วี; d รูปร่างของสามเหลี่ยม ABC โดยที่ A; B;6 ค;; d วิธีแก้ไข: a สร้างขอบเขต: เส้นตรงขนานกับแกน O; เส้นตรงขนานกับแกน O 6 เส้นผ่านจุดที่ 6 และ 6; พื้นที่เป็นรูปสามเหลี่ยม ABC รูปที่. ในการค้นหาพิกัดของจุด C จำเป็นต้องแก้ระบบสมการ รูปที่ 6 ดังนั้น C; ดังนั้นภายในขอบเขตเพื่อดูว่ามีการเปลี่ยนแปลงอย่างไรเราจึงวาดเส้นตรงขนานกับแกน O แล้วตัดกับขอบเขต เส้นตรงนี้เข้าสู่ขอบเขตตามเส้น a และออกตามเส้น 6 หรือ 6 ดังนั้น 6 ดังนั้นขอบเขต สามารถกำหนดได้โดยระบบอสมการ: 6 ตอนนี้มันง่ายที่จะกำหนดขีดจำกัดในอินทิกรัลคู่: f 6 f

4 b มาสร้างพาราโบลาตรงขนานกับแกน O กันดีกว่า ภาพที่ จงหาพิกัดของจุด A และ B โดยแก้ระบบ ± วาดเส้นตรงขนานกับแกน O แล้วตัดกันบริเวณนี้ เส้นนี้จะเข้าสู่ขอบเขตตาม พาราโบลาและใบไม้ตามแนวเส้นตรง รูปที่ ดังนั้น ขอบเขตถูกกำหนดโดยความไม่เท่าเทียมกัน f f: ดังนั้นใน เรามาสร้างพื้นที่กันเถอะ รูป: พาราโบลาสมมาตรรอบแกน O โดยมีจุดยอดที่จุดเริ่มต้น สาขาบวกของพาราโบลา y สมมาตรเทียบกับแกน O โดยมีจุดยอดที่จุดกำเนิดของพิกัด มะเดื่อ ลองหาจุดตัดกันของเส้นเหล่านี้: โดยการยกกำลังสองทั้งสองข้างของสมการที่เราได้รับ จากที่นี่ ดังนั้นเส้นจะตัดกัน ที่จุด O; และก; เมื่อลากเส้นตรงขนานกับ O แล้วตัดกันพื้นที่เราจะเห็นว่าเส้นเข้าและเส้นออก

5 ดังนั้น f f g เรามาสร้างรูปสามเหลี่ยมกัน จากภาพวาดจะชัดเจนว่าภายในพื้นที่ A เส้นตรงขนานกับ O และตัดกันพื้นที่เข้าสู่สามเหลี่ยมตามด้าน AC และออกตามด้าน AB สมการของเส้นที่ผ่าน จุดสองจุด M และ M มีรูปแบบ การใช้สูตรนี้เราจะเขียนสมการของด้าน AB และ AC: AB: มาจากไหน; 6 AC: ที่มาจาก ดังนั้น: ดังนั้น f f d เรามาสร้างขอบเขตกัน โดยเปลี่ยนสมการของขอบเขต: ลองเลือกกำลังสองที่สมบูรณ์ตามตัวแปร: สมการที่ได้จะกำหนดวงกลมรัศมีโดยมีจุดศูนย์กลางอยู่ที่ คะแนน; Fig Fig Fig ในการกำหนดขีดจำกัดของการรวมคุณจะต้องเขียนสมการของครึ่งบนและล่างของวงกลมของเส้นเข้าในพื้นที่และออกจากขอบเขต ให้เราแก้สมการดั้งเดิมด้วยความเคารพ: ±

6 เห็นได้ชัดว่าครึ่งบนของวงกลมสอดคล้องกับสมการของวงกลมล่าง ดังนั้น f f ตัวอย่าง เปลี่ยนลำดับการรวม: b 6 ; ฉ ฉ ; a c f f วิธีแก้ไข: a พื้นที่ของการอินทิเกรตถูกกำหนดโดยระบบอสมการ: มาสร้างพื้นที่กัน รูปที่ 6: ครึ่งบนของพาราโบลา ครึ่งล่างของพาราโบลา เมื่อเปลี่ยนลำดับของการอินทิเกรต อินทิกรัลจะอยู่ในรูปแบบ c f ภาพที่ 6 ลองหาพิกัดของจุดตัดของพาราโบลากับเส้นตรง: ± ดังนั้น A; ใน; ลองวาดเส้นตรงขนานกับแกน O ที่ตัดกับพื้นที่ เส้นเข้าของสิ่งนี้ลงสู่พื้นที่คือพาราโบลา เส้นทางออกเป็นเส้นตรง ดังนั้น พื้นที่ยังสามารถกำหนดได้โดยระบบอสมการ: จากนั้น f f 6

7 b ในกรณีนี้ พื้นที่ของการบูรณาการถูกกำหนดโดยระบบของความไม่เท่าเทียมกัน: 6 เรามาสร้างพื้นที่นี้ในรูปที่ 7: 6 ไฮเปอร์โบลา เส้นตรง ลองหาพิกัดของจุด A และ B ที่จุด A ดังนั้น ที่จุด B ดังนั้น ดังนั้น ก; ใน; เมื่อเปลี่ยนลำดับการรวม อินทิกรัลจะอยู่ในรูปแบบ ฉ รูปที่ 7 ค ตั้งแต่นั้นมา ค ; ลองวาดเส้นตรงขนานกับแกน O แล้วตัดกันบริเวณนั้น เส้นอินพุต 6 คือไฮเปอร์โบลาจากตำแหน่ง เส้นเอาท์พุตเป็นเส้นตรงจากตำแหน่ง 6 พื้นที่ถูกกำหนดโดยอสมการ: 6 ในที่สุดเราก็ได้ 6 6 f f ใน มาสร้างพื้นที่กัน: และ: ขอบเขตของพื้นที่ถูกกำหนดโดยสมการ ± โดยการยกกำลังสองทั้งสองด้านของสมการ เราจะได้สมการของจุดยอดพาราโบลา โคโตะ - ฝูงจะอยู่ที่จุดหนึ่ง และแกนสมมาตรคือแกน O รูปที่ ขอบเขตของขอบเขตถูกกำหนดโดยสมการต่อไปนี้: เส้นตรงที่ผ่านจุดกำเนิดของพิกัดและกิ่งบนของพาราโบลา ดังนั้น พื้นที่ของปริพันธ์ รูปที่ 7

8 เพื่อกำหนดขีดจำกัดของการอินทิเกรต เราจะหาพิกัดของจุดตัดของเส้นเขตแดน เพื่อทำสิ่งนี้ เราจะแก้ระบบสมการ ด้วยเหตุนี้ A; ใน; เมื่อเปลี่ยนลำดับอินทิเกรตเราจะนำอินทิกรัลภายนอกมาเหนือตัวแปรตัวใน ดังนั้น เราจะวาดเส้นตรงตัดกันบริเวณและขนานกับแกน Ox มันจะเข้าสู่ขอบเขตตามเส้นและออกไปตาม เส้น ดังนั้นการเปลี่ยนลำดับของการรวมเข้าด้วยกันเราได้รับ f f f ที่นี่การเปลี่ยนลำดับของการรวมทำให้การคำนวณง่ายขึ้นเนื่องจากแทนที่จะคำนวณปริพันธ์สองตัวคุณจะต้องคำนวณเพียงตัวอย่างเดียว คำนวณ; ; โดยที่พื้นที่ถูกจำกัดด้วยเส้น วิธีแก้ เรามาสร้างพื้นที่กัน รูปที่ 9: เส้นตรงที่ขนานกับแกน O และเส้นตรงที่ผ่านจุดกำเนิดของพิกัด ในการคำนวณอินทิกรัล ให้ย้ายจากอินทิกรัลคู่ไปเป็นอินทิกรัลที่ซ้ำกัน เนื่องจากพื้นที่สามารถกำหนดได้โดยระบบความไม่เท่าเทียมกัน: จากนั้นรูปที่ 9 เราคำนวณอินทิกรัลภายในก่อนโดยพิจารณาว่าเป็นค่าคงที่เนื่องจากการอินทิเกรตดำเนินการกับตัวแปร: ตอนนี้ยังคงคำนวณอินทิกรัลภายนอกที่เป็นผลลัพธ์:

9 ดังนั้น ตัวอย่างการคำนวณวิธีแก้ปัญหา สร้างขอบเขต: แกน O เป็นเส้นตรงขนานกับแกน O ซึ่งเป็นเส้นตรงที่ผ่านจุดกำเนิดของพิกัด มะเดื่อ เส้นตรงและตัดกันที่จุด A; เมื่อผ่านไปยังอินทิกรัลคู่แล้วคำนวณเราจะได้ว่ามันถูกจำกัดด้วยเส้นตามสูตรการลดขนาด รูปที่ 9

10 ปัญหาสำหรับการแก้ปัญหาอย่างอิสระ จัดขีดจำกัดของการอินทิเกรตในอินทิกรัลซ้ำ โดยที่ f จะลดลงหากพื้นที่ถูกจำกัดด้วยเส้นตรง: a; ข; วี; กรัม; d สามเหลี่ยม ABC โดยที่ A; ใน; กับ; เปลี่ยนลำดับการรวม: a f ; ขฉ ; ในฉ; g f คำนวณปริพันธ์คู่โดยสมมติว่าพื้นที่ถูกจำกัดด้วยเส้นที่ระบุ: a; 7; ข; ; วี; ; กรัมอี; 6 คำตอบ ฉ ; ขฉ ; ใน gf ; d af ; ข ฉ ; ในฉ; ก เอฟ ก; 7 ข; วี; ฉ 6 กรัม อี ฉ ;

11 จำนวนเต็มคู่ในพิกัดเชิงขั้ว หากให้ทั้งระบบพิกัดคาร์ทีเซียนและพิกัดเชิงขั้วบนระนาบและขั้วเกิดขึ้นพร้อมกับจุดกำเนิดของพิกัดและแกนเชิงขั้วอยู่ในแนวเดียวกับแกน Ox จากนั้นเพื่อไปยังพิกัดเชิงขั้วให้ใช้สูตร รูปที่. ยิ่งไปกว่านั้น หากพื้นที่ถูกจำกัดด้วยรังสี α β และเส้นโค้ง รูป f β α f เฉลยของตัวอย่าง ตัวอย่าง คำนวณ > เฉลย เรามาสร้างขอบเขตในรูป: วงกลมรัศมี เส้นตรงที่ผ่านจุดกำเนิดของพิกัด เนื่องจากขอบเขต เป็นส่วนหนึ่งของวงกลมจึงสะดวกในการไปยังพิกัดเชิงขั้ว ในกรณีนี้ ขั้วเข้ากันได้กับจุด O; และให้แกนเชิงขั้วอยู่ตามแนวแกน O จากนั้นโดยที่พื้นที่ถูกจำกัดด้วยเส้น Fig ตอนนี้เราต้องอธิบายพื้นที่ในระบบพิกัดเชิงขั้ว มุมภายในพื้นที่แปรผันจาก cm Fig ตรง k มีความโน้มเอียงไปที่แกน O

12 ที่มุมซึ่งมีแทนเจนต์เท่ากับ k ดังนั้น tg ; tg จากที่นี่; ดังนั้น ภายในขอบเขต รังสีที่เล็ดลอดออกมาจากขั้ว O และจุดตัดกันจะทิ้งขอบเขตไว้ตามวงกลม ซึ่งสมการในพิกัดเชิงขั้วจะมีรูปแบบ ดังนั้น ขอบเขตจึงอธิบายด้วยระบบความไม่เท่าเทียมกัน ตอนนี้จึงวางได้ง่าย ขีดจำกัดในอินทิกรัลซ้ำแล้วคำนวณ ตัวอย่าง คำนวณ e โดยที่วงแหวน วิธีแก้ไข เนื่องจากขอบเขตถูกจำกัดด้วยวงกลม 9 และ 9 มะเดื่อ สะดวกในการสลับไปใช้พิกัดเชิงขั้ว: จากนั้นสมการขอบเขตจะอยู่ในรูปแบบ 9 มะเดื่อ เพื่อกำหนดขอบเขตของการอินทิเกรตในอินทิกรัลซ้ำเราสังเกตว่าภายในขอบเขตมุมจะใช้ค่าทั้งหมดจากถึงให้เราวาดรังสีจากจุดกำเนิดของพิกัดที่ตัดกับขอบเขต มันจะเข้าสู่ขอบเขตตามเส้น และใบไม้ไปตามเส้น ดังนี้ว่า แล้ว

13 9 9 9 eee eee eee eee ตัวอย่าง คำนวณว่าถูกกำหนดโดยความไม่เท่าเทียมกันหรือไม่: วิธีแก้ไข เรามาสร้างขอบเขตกัน เพื่อทำสิ่งนี้ เราแปลงสมการของขอบเขต: ดังนั้น ขอบเขตจึงเป็นวงกลมรัศมีที่มีจุดศูนย์กลางอยู่ที่จุดหนึ่ง ตั้งแต่นั้นมาครึ่งบนของวงกลมคือรูป มาดูพิกัดเชิงขั้วกันดีกว่า: รูปสมการขอบเขตในพิกัดเชิงขั้วจะอยู่ในรูปแบบ สมมติว่าเราได้ พื้นที่นั้นตั้งอยู่ทั้งหมดในไตรมาสแรก ดังนั้นในพิกัดเชิงขั้ว พื้นที่จึงกำหนดโดย อสมการ ตอนนี้เราสามารถคำนวณอินทิกรัลสองเท่าได้แล้ว

14 ปัญหาสำหรับการแก้ปัญหาอย่างอิสระ คำนวณโดยการเคลื่อนที่ไปยังพิกัดเชิงขั้ว: โดยที่ครึ่งบนของวงกลม 6 โดยที่พื้นที่นั้นเป็นไปตามความไม่เท่าเทียมกัน โดยที่พื้นที่ถูกจำกัดด้วยเส้นตรง 9 6 โดยถูกจำกัดด้วยเส้นที่ 6 โดยที่พื้นที่ถูกจำกัดด้วยเส้นโค้ง คำตอบ; ; ; ; การประยุกต์ใช้อินทิกรัลสองเท่าใช้ในการคำนวณ: และพื้นที่ของรูปเครื่องบินที่ถูกจำกัดโดยพื้นที่: S; b ปริมาตรของทรงกระบอกที่ถูกจำกัดจากด้านบนด้วยพื้นผิวต่อเนื่อง f จากด้านล่างโดยระนาบ และจากด้านข้างด้วยพื้นผิวทรงกระบอกตรงที่ตัดพื้นที่บนระนาบ O:

15f; ในพื้นที่ผิวที่กำหนดโดยสมการ f ซึ่งเส้นโครงบนระนาบ O คือขอบเขต: σ นอกจากนี้ยังใช้อินทิกรัลคู่ในกลศาสตร์เพื่อคำนวณ: และมวลของแผ่นเรียบที่ครอบครองบริเวณของระนาบ O และ มีความหนาแน่นของพื้นผิวแปรผัน γ γ: M γ ; b โมเมนต์ทางสถิติของแผ่นที่สัมพันธ์กับแกน O และ O: ; เอ็ม γ ; M γ ในพิกัดจุดศูนย์ถ่วงของแผ่น: γ M c; M γ คำตอบของตัวอย่าง ц M M γ γ 6 ตัวอย่าง จงหาพื้นที่ของขอบเขตที่ล้อมรอบด้วยเส้น วิธีแก้ไข เรามาสร้างขอบเขตกัน สมการนี้ให้นิยามพาราโบลา ซึ่งเป็นสมการของเส้นตรงที่ลากผ่านจุดกำเนิดของพิกัด มะเดื่อ เพื่อหา จุดตัดกันของเส้นเหล่านี้เราแก้ระบบสมการ: จากที่นี่แล้วดังนั้นเส้นตรงตัดพาราโบลาที่จุด และก; การใช้สูตร S Fig ตัวอย่าง ค้นหาพื้นที่ของภาพที่ล้อมรอบด้วยเส้นนอกวงกลมวงแรก

16 วิธีแก้ สมการระบุวงกลมรัศมีโดยมีจุดศูนย์กลางอยู่ที่จุดกำเนิดของพิกัด สมการระบุวงกลมรัศมีโดยมีจุดศูนย์กลางอยู่ที่จุด ให้เราแก้ระบบสมการด้วยกัน ± ดังนั้น; ก; B ขอบเขต AmBn สามารถระบุได้ด้วยความไม่เท่าเทียมกัน โดยใช้สูตร 6 S ตัวอย่าง ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยระนาบพิกัดและระนาบ วิธีแก้ไข มาสร้างลำตัวกัน รูปที่ 7 และการฉายภาพของมันลงบนระนาบ O รูปที่ 6

17 ตามสูตร รูปที่ 7 รูปที่ ในตัวอย่างนี้ พื้นที่คือสามเหลี่ยม OAB แสดงในรูปที่ และพื้นผิวถูกกำหนดโดยสมการของระนาบจากที่ ตัวอย่างนี้ จงหาปริมาตรของวัตถุที่ถูกจำกัดด้วยระนาบพิกัด ของระนาบและพื้นผิว วิธีแก้ไข ตัวถังดังแสดงในรูปที่ 9 ระนาบวิ่งขนานกับแกน O พาราโบลอยด์ที่มีจุดยอดอยู่ที่จุด;; เส้นโครงของร่างกายบนระนาบ O คือสามเหลี่ยม ABO รูปที่ AB เส้นตัดกันของระนาบกับระนาบ ดังนั้นสมการของเส้นตรง AB: โดยที่ 7

18 การใช้สูตร รูปที่ 9 รูปที่ มีทรงกระบอก 6 ตัวอย่าง ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพาราโบลาและระนาบและวิธีแก้ปัญหา ตัวถังแสดงไว้ในรูปที่ เพื่อความสะดวกในการกำหนดขีดจำกัดของการรวมเข้าด้วยกัน เราจึงสร้างเส้นโครงของ ลำตัวขึ้นสู่ระนาบ O Fig. ใช้สูตร Fig. Fig.

19 7 6 ตัวอย่างที่ 6 จงหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว 7 วิธีแก้ วัตถุนี้ถูกล้อมรอบด้วยพาราโบลอยด์สองตัว ภาพที่ เส้นตัดของพาราโบลอยด์ถูกกำหนดโดยระบบสมการ จากสมการแรก ดังนั้นเส้นตัดจึงเป็นวงกลม รัศมีที่วางอยู่บนระนาบ: เส้นโครงของเส้นนี้บนระนาบ O ก็เป็นวงกลมเช่นกัน ดังนั้นจึงสะดวกที่จะไปที่พิกัดเชิงขั้ว มะเดื่อ ปริมาตรของวัตถุสามารถคำนวณได้เป็นผลต่างระหว่างปริมาตรของทรงกระบอกสองกระบอก เนื้อความ: ตัวอย่างที่ 7 หาพื้นที่ผิวของทรงกลมภายในทรงกระบอก 9 วิธีแก้ปัญหา ทรงกระบอกตัดสองส่วนบนพื้นผิวของทรงกลมที่มีความสมมาตรสัมพันธ์กับระนาบ O รูป เนื่องจากความสมมาตรก็เพียงพอที่จะคำนวณหา พื้นที่ผิวของเฉพาะ "หมวก" ด้านบนและเพิ่มผลลัพธ์เป็นสองเท่า 9

20 ในการคำนวณ เราใช้สูตร เนื่องจากมันมีอนุพันธ์ย่อยอยู่ด้วย เราจึงคำนวณ และเราได้จากสมการของทรงกลม แล้วก็รูป ดังนั้นตามสูตร σ การฉายภาพพื้นผิวลงบนระนาบ วงกลม O จึงไปได้สะดวก ถึงพิกัดเชิงขั้ว ในระบบพิกัดเชิงขั้วสมการของวงกลมจะมีลักษณะดังนี้ ดังนั้นในพิกัดเชิงขั้ว σ 9 ดังนั้น 9 จะยอมรับ เนื่องจากเราพิจารณาพื้นที่ของ "หมวก" ด้านบนเท่านั้น พื้นที่ผิวทั้งหมดจะเท่ากับ σ σ n ตัวอย่าง จงหาจุดศูนย์ถ่วงของแผ่น ABC ที่เป็นเนื้อเดียวกัน ถ้า A;- B; ค; ;- วิธีแก้ ในการคำนวณพิกัดของจุดศูนย์ถ่วง เราจะใช้สูตร 6 เนื่องจากแผ่นเป็นเนื้อเดียวกัน ความหนาแน่นของพื้นผิว γ จึงคงที่ ดังนั้นสูตรจะอยู่ในรูปแบบ q ทีเอส

21 จากรูปในรูป เห็นได้ชัดว่าแผ่นมีรูปร่างเป็นรูปสี่เหลี่ยมคางหมูและสมมาตรเมื่อเทียบกับแกน O ดังนั้น ให้เราเขียนสมการของเส้นตรง BC และ A โดยใช้สูตรที่กำหนดสมการของ เส้นตรงที่ผ่านจุดที่กำหนดสองจุด: c BC: ; A: รูปที่ให้เราแยกกันคำนวณเศษและส่วนของเศษส่วนที่กำหนดพิกัด: q 9 ตัวส่วนมีอินทิกรัลเท่ากับพื้นที่ของภูมิภาคและพื้นที่ของสี่เหลี่ยมคางหมู ABC ดังนั้น ชั่วโมง ; คุณสามารถคำนวณอินทิกรัล AB C ได้โดยตรง ดังนั้น c; ตัวอย่างที่ 9 จงหามวลของครึ่งบนของวงรี ถ้าความหนาแน่นของแต่ละจุดเท่ากับพิกัดของจุด b a วิธีแก้ ความหนาแน่นที่แต่ละจุดเท่ากับพิกัด γ ตามสูตร M γ สำหรับครึ่งบนของ วงรี รูปที่ 6 b ดังนั้น รูปที่ 6

22 M a a a b a b a a b a a b a a a b ปัญหาสำหรับการแก้ปัญหาอิสระ a ab ค้นหาพื้นที่ของรูปที่ล้อมรอบด้วยเส้น: a; ข; ใน; กรัม ; d ค้นหาปริมาตรของร่างกายที่ล้อมรอบด้วยพื้นผิว: a; ข; ใน; d ค้นหาพื้นที่ของพื้นผิวที่ระบุ: a ของส่วนของระนาบ 6 ที่อยู่ในออคแทนต์แรก b ส่วนหนึ่งของระนาบ a ตัดออกด้วยกระบอกสูบ a; ในพาราโบลาภายในกระบอกสูบ g ของพาราโบลาที่ตัดด้วยทรงกระบอกพาราโบลาและระนาบ จงหาจุดศูนย์ถ่วงของ ABC ทรงสี่เหลี่ยมคางหมู โดยที่ A; บี; ค; ; ถ้าความหนาแน่นของแต่ละจุดเท่ากับค่า abscissa ของจุดนี้ จงหาจุดศูนย์ถ่วงของรูปเนื้อเดียวกันที่ล้อมรอบด้วยพาราโบลาและเส้นตรง 6 จงหามวลของแผ่นรัศมีวงกลม ถ้าความหนาแน่นของพื้นผิวในแต่ละจุดเป็นสัดส่วน ไปยังระยะห่างจากศูนย์กลางของวงกลม ตอบ ก; ข; วี; กรัม ; วัน 6 ถึง 6; ข; ใน; ก.ก

23 ก; ข ; วี; g c c c c 6 6 k การคำนวณจำนวนเต็มสามตัวในพิกัดคาร์ทีเซียน ในการคำนวณอินทิกรัลสามตัว จะแสดงเป็นอินทิกรัลสามตัว: วิธีแก้ตัวอย่าง ตัวอย่าง ไปจาก f b a f f ถึงสามและกำหนดขีดจำกัดของอินทิเกรตหากพื้นที่ถูกจำกัดด้วย: ระนาบและ ประสานงานเครื่องบิน ข กรวยและระนาบ h; ในลูกบอล วิธีแก้ไข a ลองสร้างขอบเขตและการฉายภาพของขอบเขตนี้ลงบนระนาบ O รูปที่ 7 เส้นตรง AB เป็นเส้นตัดระหว่างระนาบกับระนาบ ดังนั้นสมการของมันคือ OAB รูปที่ 7 รูปที่จากรูป . จะสังเกตง่ายๆ ว่า โดยลากเส้นตรงขนานกับแกน O แล้วตัดกับรูปสามเหลี่ยม OAB เราสังเกตเห็นว่าเธอเข้ามาตามเส้นแล้วออกไปตามเส้น

24 เพื่อหาขีดจำกัดของการเปลี่ยนแปลง เราวาดเส้นตรงขนานกับแกน O แล้วตัดกันพื้นที่ รูปที่ 7 มันเข้าสู่พื้นที่ตามพื้นผิวและออกไปตามพื้นผิว ดังนั้น พื้นที่จึงสามารถอธิบายได้ด้วยระบบของ ความไม่เท่าเทียมกัน 6 ดังนั้น f f 6 b ในการกำหนดขีด จำกัด ในปริพันธ์สามเราสร้างพื้นที่และการฉายภาพของมันบนระนาบ O บริเวณ รูปที่ 9 สมการของเส้นที่ล้อมรอบพื้นที่นั้นได้มาจากการแก้ระบบสมการ h h รูปที่ 9 นั่น คือ วงกลมรัศมี h โดยมีจุดศูนย์กลางอยู่ที่จุดกำเนิดของพิกัด ลากเส้นตรงขนานกับ O และ O ตัดกัน แล้วเราจะได้สิ่งที่ระบบอสมการอธิบายไว้ h h h h h ดังนั้น h h h h f f

25 คุณสามารถเลือกลำดับอินทิกรัลอื่นในปริพันธ์สามอันได้ จากนั้น ขีดจำกัดของอินทิกรัลก็จะเปลี่ยนไปตามไปด้วย ตัวอย่างเช่น ลองจินตนาการถึงอินทิกรัลดั้งเดิมในรูปแบบ c f เพื่อกำหนดขีดจำกัดของอินทิกรัล เราจะฉายภาพลงบนระนาบ O และลากเส้นตรงขนานกับ O และ O แล้วตัดกันตามลำดับและรูปที่ ในกรณีนี้ มันถูกกำหนดโดยความไม่เท่าเทียมกัน: h ดังนั้น h f f Fig c ลองสร้างพื้นที่และการฉายภาพของมันลงบนระนาบ O Fig Fig จากภาพวาดที่ได้คือ ชัดเจนว่า

26 f f f f ตัวอย่าง คำนวณว่าวัตถุถูกจำกัดด้วยระนาบพิกัดของระนาบและกรวย วิธีแก้ไข ลองสร้างวัตถุและการฉายภาพของมันลงบนระนาบ O Fig. จากภาพวาดจะเห็นได้ชัดว่าอธิบายได้ด้วยความไม่เท่าเทียมกัน: รูปที่ 6 6

27 ปัญหาสำหรับการแก้ปัญหาอย่างอิสระ เปลี่ยนจาก f ไปเป็นปริพันธ์สามตัวแล้วกำหนดขีดจำกัดของอินทิเกรตถ้าตัวถูกจำกัด: a โดยทรงรี; 9 ข พาราโบลาลอยด์และระนาบ; ในระนาบพิกัดและระนาบ 6 คำนวณว่าร่างกายถูกจำกัดด้วยระนาบและทรงกลม คำนวณว่าร่างกายถูกจำกัดด้วยระนาบหรือไม่ คำนวณด้วยกรวย คำตอบ 9 ถ้าร่างกายถูกจำกัดด้วยระนาบ a f ; ขฉ ; ใน f 6 การเปลี่ยนแปลงของตัวแปรในพิกัดทรงกระบอกและทรงกลมสามเท่า สูตรสำหรับการเปลี่ยนไปใช้พิกัดทรงกระบอก รูป: ; ; ; สูตรการเปลี่ยนไปใช้พิกัดทรงกลม θ r รูป: r θ ; ร θ ; ร θ ; r θrθ ที่นี่; θ ; ร 7

28 เฉลยตัวอย่าง ตัวอย่าง คำนวณ Fig Fig หากถูกจำกัดด้วยกรวยและระนาบ วิธีแก้ วัตถุจะปรากฎในรูปนี้ เส้นตัดกันของกรวยและระนาบมีสมการ te ดังนั้น การฉายวัตถุลงบนวงกลม O ในระนาบ Fig6 Fig Fig 6 มาดูพิกัดทรงกระบอกกันดีกว่า: ; ; ; ในพิกัดเหล่านี้ สมการของวงกลมที่แสดงในรูปที่ 6 สมการของกรวยและร่างกายถูกกำหนดโดยอสมการ ; ดังนั้น

29 v ตัวอย่าง คำนวณว่าร่างกายถูกจำกัดด้วยพื้นผิวหรือไม่ สารละลาย สร้างขอบเขต; ระนาบ ในการสร้างพื้นผิว เราแปลงสมการ: สมการนี้ให้นิยามทรงกระบอกทรงกลมที่ฐานซึ่งมีวงกลมรัศมีโดยมีจุดศูนย์กลางอยู่ที่จุด;; ดังนั้นขอบเขตการรวมจึงเป็นทรงกระบอก รูปที่ 7 ดังนั้นจึงสะดวกที่จะใช้พิกัดทรงกระบอก ในพิกัดเหล่านี้ สมการของพื้นผิวทรงกระบอกที่ล้อมรอบขอบเขตการรวมจะอยู่ในรูปแบบ นั่นคือ จากที่ไหน ขึ้นอยู่กับสิ่งนี้ ภูมิภาคสามารถอธิบายได้ด้วยระบบความไม่เท่าเทียมกัน ; รูปที่ 7 9

30 ดังนั้น ตัวอย่าง จงคำนวณว่าส่วนของร่างกายคือครึ่งบนของลูกบอล คำตอบ เนื่องจากบริเวณนี้ของการรวมเป็นส่วนหนึ่งของลูกบอล จึงสะดวกที่จะไปยังพิกัดทรงกลม: r r r r r r r r r r r r r θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ ปัญหาสำหรับการแก้ปัญหาอิสระ คำนวณหากมีพื้นผิวจำกัด คำนวณตำแหน่งที่ล้อมรอบด้วยพื้นผิว

31 คำนวณ คำนวณหากจำกัดอยู่ที่พื้นผิวหากลูกบอล ตอบ การใช้งานของจำนวนเต็มสามตัว อินทิกรัลสามใช้ในการคำนวณ: และปริมาตรของตัววัตถุ Ω: ; 7 Ω b มวลกายซึ่งครอบครองพื้นที่ Ω โดยมีความหนาแน่นปริมาตรแปรผัน γ: M γ ; Ω ในพิกัดของจุดศูนย์ถ่วงของร่างกาย Ω: q γ M Ω q γ 9 M Ω q γ M Ω โดยที่ M คือมวลของร่างกาย หากร่างกายเป็นเนื้อเดียวกันดังนั้นในสูตร 9 เราสามารถใส่γ ; M เฉลยตัวอย่าง ตัวอย่าง ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยทรงกระบอกและระนาบ วิธีแก้ปัญหา วัตถุและการฉายภาพของมันบนระนาบ O แสดงในรูปที่ มะเดื่อ ในการค้นหาพิกัดของจุด A และ B เราจะแก้ระบบสมการ : :

32±เอ; บี; ดังนั้นขอบเขต Ω จึงอธิบายโดยระบบอสมการ ; การใช้สูตร 7 Ω ตัวอย่าง จงหามวลของวัตถุที่ล้อมรอบด้วยระนาบ ถ้าความหนาแน่นในแต่ละจุดคือ γ วิธีแก้ไข ลองสร้างวัตถุ Ω และเส้นโครงของมันลงบนระนาบ O รูปที่ 9 รูปที่ 9 เครื่องบินตัดกับระนาบตามแนวเส้นตรง เส้น การแก้ระบบเราได้รับพิกัดของจุด A; ดังนั้น ตัว Ω จึงถูกอธิบายโดยระบบความไม่เท่าเทียมกัน ; การใช้สูตรมวลกาย M Ω ตัวอย่าง คำนวณมวลของวัตถุที่ล้อมรอบด้วยระนาบ 9 และทรงกระบอกพาราโบลา ถ้าความหนาแน่นที่แต่ละจุดเป็นสัดส่วนกับ abscissa และที่ระยะห่างหนึ่งหน่วยจากระนาบ O เท่ากับ

33 ความหนาแน่นของสารละลายเป็นสัดส่วนกับ abscissa ดังนั้น k γ ที่ระยะหน่วยจากระนาบ O ความหนาแน่นจะเท่ากับ ดังนั้นสำหรับ γ จากนั้น k k ดังนั้น γ สร้างตัว Ω และเส้นโครงของมันลงบนระนาบ O Fig Fig เพื่อหาพิกัดของจุด A ให้แก้ระบบสมการ 9 A ดังนั้น พื้นที่สามารถกำหนดได้โดยระบบอสมการ Ω Ω 9 ตามสูตร มวลของวัตถุเท่ากับ Ω M ตัวอย่าง จงหาพิกัดของจุดศูนย์ถ่วงของวัตถุที่ล้อมรอบด้วยครึ่งล่าง ของทรงกลมและพาราโบลอยด์ ถ้าความหนาแน่นของแต่ละจุดเป็นสัดส่วนกับกำลังสองของระยะห่างจากแกน O

34 วิธีแก้ เรามาสร้างตัวกันก่อน จุดยอดของพาราโบลาคือจุด ; สมการนี้สามารถแปลงเป็นรูปแบบที่กำหนดทรงกลมรัศมีโดยมีจุดศูนย์กลางอยู่ที่จุดหนึ่ง ; วัตถุจึงมีรูปแบบดังแสดงในรูปที่ เส้นโครงของวัตถุนี้บนระนาบ O จะเป็นวงกลม สมการนี้สามารถหาได้โดยการแก้ระบบสมการ ในระนาบ สมการของเส้นตัดจะมีรูปแบบ สมการของการฉายภาพของร่างกาย Ω บนเครื่องบินมีรูปแบบเดียวกัน Ω มะเดื่อ เนื่องจากวงกลมสะดวกเมื่อคำนวณ ให้ไปที่พิกัดทรงกระบอก ; ; ในพิกัดเหล่านี้ สมการของขอบเขต Ω มีรูปแบบ และมุมเป็นไปตามเงื่อนไข สมการของพาราโบลอยด์ในพิกัดทรงกระบอกจาก โดยที่ สมการของทรงกลม ± สำหรับครึ่งล่าง ความหนาแน่นของตัวแปรตามเงื่อนไขของปัญหาจะเป็นสัดส่วนกับกำลังสองของระยะห่างจากแกน O ที่ γ k In พิกัดทรงกระบอก γ k เนื่องจากร่างกายมีความสมมาตรเกี่ยวกับแกน O จึงเห็นได้ชัดว่าจุดศูนย์ถ่วงอยู่บนแกนนี้คือ q; q ในการคำนวณ q เราใช้สูตร 9: q γ M Ω ก่อนอื่นให้เราคำนวณมวลของร่างกาย M [สูตร ]:

35 6 k k k k k k k M γ Ω Ω Ω ทีนี้ มาคำนวณ Ω Ω Ω γ k k k k k k k k ตามสูตร k k c ดังนั้นจุดศูนย์ถ่วงของร่างกายจึงมีพิกัด ; 7

36 ปัญหาสำหรับการแก้ปัญหาอย่างอิสระ 6 ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วย: ระนาบ; ข พาราโบลอยด์และระนาบ ในพื้นผิวและ 6 ค้นหามวลของวัตถุที่มีจำกัด: a คูณทรงกลม ถ้าความหนาแน่นคือ γ k ; b พื้นผิว ถ้าความหนาแน่นเป็น γ k ; ในกรวยและระนาบ b ถ้าความหนาแน่นเป็นสัดส่วนกับพิกัดของจุดและที่ระยะห่างหนึ่งหน่วยจากระนาบ O เท่ากับ γ ​​6 ค้นหาพิกัดของจุดศูนย์ถ่วงของวัตถุเนื้อเดียวกันที่ล้อมรอบด้วยระนาบ a คำตอบ 6 ก; ข; ใน 6 9 k γb 6 a k ; ข; ที่ 6 6 C;; 6

37 ตัวเลือก ภาคผนวก ตัวเลือกสำหรับการบ้านส่วนบุคคล ค้นหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น ค้นหาพื้นที่ผิวของทรงกระบอกที่อยู่ภายในทรงกระบอก ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว ค้นหามวลของวัตถุที่ล้อมรอบด้วย a ทรงกลมและพาราโบลอยด์ถ้าความหนาแน่น ณ จุดใด ๆ เท่ากับการทาของจุดนี้ ตัวเลือก จงหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้นตรงและไซนัสอยด์ครึ่งคลื่นหนึ่งอัน จงหาพื้นที่ผิวของกรวยที่ถูกตัดออกด้วย ระนาบ ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว ค้นหามวลของวัตถุที่ล้อมรอบด้วยส่วนหนึ่งของลูกบอลรัศมีที่อยู่ในออคแทนต์แรก ถ้าความหนาแน่น ณ จุดใด ๆ เท่ากับระยะทางจากจุดถึงระนาบ O ตัวเลือก ค้นหา จุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น จงหาพื้นที่ผิวของกรวยภายในทรงกระบอก 9 จงหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว 9 9 จงหามวลของวัตถุที่ถูกล้อมรอบด้วยชั้นทรงกลมระหว่างพื้นผิว 9 และ 6 ถ้าความหนาแน่นของแต่ละจุดแปรผกผันกับระยะทางจากจุดถึงจุดกำเนิดของพิกัด ตัวเลือก ค้นหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้นตรง 6 > ค้นหาพื้นที่ผิวที่อยู่ภายในทรงกระบอก 6 ค้นหาปริมาตรของ a 7. ร่างกายถูกล้อมรอบด้วยพื้นผิว

38 จงหามวลของวัตถุที่ล้อมรอบด้วยทรงกระบอกกลมด้านขวาซึ่งมีรัศมีความสูง ถ้าความหนาแน่นของแต่ละจุดเท่ากับกำลังสองของระยะทางจากจุดหนึ่งไปยังแกนสมมาตรของทรงกระบอก ทางเลือก หาจุดศูนย์ถ่วงของ a รูปร่างแบนล้อมรอบด้วยวงกลมที่มีศูนย์กลางอยู่ที่จุดกำเนิดของพิกัดที่มีรัศมีและรังสีสองเส้นซึ่งอยู่ในตำแหน่งสมมาตรสัมพันธ์กับแกน O และเกิดเป็นมุมซึ่งกันและกัน ค้นหาพื้นที่ผิวของกรวยที่อยู่ภายในทรงกระบอก หาปริมาตรของวัตถุที่ล้อมรอบ โดยพื้นผิว จงหามวลของวัตถุที่ล้อมรอบด้วยระนาบพิกัดและระนาบ 6 ถ้าความหนาแน่นในแต่ละจุดเท่ากับค่าแอบซิสซาของจุดนี้ ทางเลือกที่ 6 จงหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยแกน O และส่วนบนของ วงรี b a ค้นหาพื้นที่ผิวของทรงกระบอกที่ถูกตัดออกด้วยระนาบ ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว 6 ค้นหามวลของวัตถุที่ล้อมรอบด้วยพื้นผิว 6 ถ้าความหนาแน่นในแต่ละจุดเท่ากับการประยุกต์ของจุดนี้ ตัวเลือกที่ 7 ค้นหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยคาร์ดิโอด์ 7 ค้นหาพื้นที่ผิวของกรวยที่ตัดด้วยทรงกระบอก คำแนะนำ ไปที่พิกัดเชิงขั้ว ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว ค้นหามวลของวัตถุที่ล้อมรอบด้วย ตามพื้นผิว > ถ้าความหนาแน่นเท่ากับพิกัดของจุด ตัวเลือก ค้นหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น p

39 หาพื้นที่ผิวของพาราโบลอยด์ภายในทรงกระบอก หาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว 6 จงหามวลของวัตถุที่ล้อมรอบด้วยพื้นผิว ถ้าความหนาแน่นในแต่ละจุดเท่ากัน ตัวเลือกที่ 9 หาจุดศูนย์ถ่วงของวัตถุแบน รูปที่ล้อมรอบด้วยเส้น 9 9 > หาพื้นที่ผิวของวัตถุที่ล้อมรอบด้วยทรงกลมและพาราโบลอยด์ จงหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว 6 9 นอกทรงกระบอก จงหามวลของวัตถุที่ล้อมรอบด้วยชั้นทรงกลมระหว่าง พื้นผิว 6 ถ้าความหนาแน่นแปรผกผันกับระยะห่างของจุดจากจุดกำเนิดของพิกัด ตัวเลือก ค้นหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้นและเส้นตรง OA ที่ผ่านจุดกำเนิดของพิกัดและจุด A ค้นหาพื้นที่ผิวของทรงกลมที่ถูกตัดออกด้วยทรงกระบอก ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว ภายในกระบอกสูบ ค้นหามวลของวัตถุที่ล้อมรอบด้วยลูกบอลที่มีรัศมี ถ้าความหนาแน่นเป็นสัดส่วนกับกำลังสามของระยะห่างจากศูนย์กลางของลูกบอล และที่ระยะหนึ่งหน่วยเท่ากับ γ ตัวเลือก ค้นหาจุดศูนย์ถ่วงของรูปร่างแบนที่ล้อมรอบด้วยเส้น 6 ค้นหาพื้นที่ผิวของทรงกระบอกระหว่างระนาบ ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว ค้นหามวลของวัตถุที่ล้อมรอบด้วยพื้นผิวทรงกระบอกและระนาบ ถ้า ความหนาแน่นเท่ากับพิกัดของจุดที่ 9

40 ตัวเลือก หาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยคาร์ดิโอด์ ค้นหาพื้นที่ผิวของลูกบอลที่อยู่ภายในทรงกระบอก ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว ค้นหามวลของวัตถุที่ล้อมรอบด้วยค่าออคแทนต์ของลูกบอล โดยพิกัดระนาบและระนาบ ถ้าความหนาแน่นในแต่ละจุดเท่ากับการประยุกต์ของจุดนี้ ทางเลือก หาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น หาพื้นที่พื้นผิวของพาราโบลาลอยด์ที่อยู่ระหว่างทรงกระบอกกับระนาบ c a b หาค่า มวลของวัตถุที่ล้อมรอบด้วยพาราโบลาลอยด์และระนาบถ้าความหนาแน่นเท่ากับผลรวมของกำลังสองของพิกัดของจุด ตัวเลือก ค้นหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น หาพื้นที่ผิวของทรงกระบอก ที่อยู่ระหว่างระนาบ O และพื้นผิว จงหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว จงหามวลของวัตถุที่ล้อมรอบด้วยทรงกระบอก 6 ถ้าความหนาแน่นเป็นสัดส่วนกับกำลังสองของระยะทางจากจุดถึงแกนของทรงกระบอก ตัวเลือก หา จุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น α α tg tg ค้นหาพื้นที่ผิวของกรวยที่อยู่ภายในทรงกระบอก ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว

41 ค้นหามวลของวัตถุที่ล้อมรอบด้วยพื้นผิว > ถ้าความหนาแน่นเท่ากับพิกัดของจุด ตัวเลือก 6 ค้นหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น 6 ค้นหาพื้นที่ผิวของลูกบอล 6 ภายในกระบอกสูบ ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว b a a b ค้นหามวลของวัตถุที่ล้อมรอบด้วยพื้นผิวหากความหนาแน่นเท่ากับการประยุกต์ของจุด ตัวเลือกที่ 7 ค้นหาจุดศูนย์ถ่วงของสามเหลี่ยมหน้าจั่วกับขา ถ้าความหนาแน่นที่แต่ละจุด จุดเป็นสัดส่วนกับกำลังสองของระยะห่างจากจุดยอดของมุมขวา หาพื้นที่ผิวของกรวยที่ตัดออกด้วยทรงกระบอก คำแนะนำ ไปที่พิกัดเชิงขั้ว ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว 9 ค้นหามวลของ บอลรัศมี ถ้าความหนาแน่นเป็นสัดส่วนกับลูกบาศก์ของระยะทางจากจุดศูนย์กลางของลูกบอลและต่อหน่วยระยะทางเท่ากับ γ ทางเลือก หาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น หาพื้นที่ผิวของ พาราโบลอยด์ที่อยู่ในอัฒภาคแรก พาราโบลอยด์ถูกล้อมรอบด้วยระนาบ 6 จงหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว 6 จงหามวลของส่วนหนึ่งของลูกบอลรัศมีที่อยู่ในอัฒจันทร์แรก ถ้าความหนาแน่นของแต่ละจุดเท่ากับ ระยะห่างจากระนาบ O ตัวเลือกที่ 9 หาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น หาพื้นที่ผิวของวัตถุที่ล้อมรอบด้วยทรงกลมและพาราโบลาลอยด์

42 จงหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว จงหามวลของวัตถุที่ล้อมรอบด้วยทรงกระบอกตรงที่มีรัศมีความสูง ถ้าความหนาแน่นเท่ากับกำลังสองของระยะห่างของจุดจากจุดศูนย์กลางของฐานของทรงกระบอก ตัวเลือก หาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น > หาพื้นที่ผิวของทรงกลม 9 ตัดออกด้วยทรงกระบอก หาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว หามวลของลูกบอลรัศมีถ้าความหนาแน่นเป็น เป็นสัดส่วนกับลูกบาศก์ของระยะทางจากจุดศูนย์กลางและที่ระยะหนึ่งหน่วยเท่ากับ γ ทางเลือก จงหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น ± tg 6 จงหาพื้นที่ผิวของทรงกระบอกภายในทรงกระบอก หา ปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิวภายในทรงกระบอก จงหามวลของวัตถุที่ล้อมรอบด้วยส่วนร่วมของลูกบอลสองลูก ถ้าความหนาแน่นเป็นสัดส่วนกับระยะทางจากจุดถึงระนาบ O ทางเลือก จงหาจุดศูนย์ถ่วงของวัตถุแบนที่ล้อมรอบด้วย คาร์ดิออยด์ หาพื้นที่ผิวของกรวยที่ถูกตัดออกด้วยระนาบ หาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิวด้านนอกทรงกระบอก 6 จงหามวลของส่วนหนึ่งของลูกบอลรัศมีที่อยู่ในออคแทนต์แรกถ้าความหนาแน่นในแต่ละจุด เท่ากับระยะห่างจากระนาบ O

43 ตัวเลือก จงหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น จงหาพื้นที่ผิวของพาราโบลาลอยด์ 6 ที่อยู่ระหว่างทรงกระบอกกับระนาบ จงหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว จงหามวลของวัตถุที่ล้อมรอบด้วยทรงกลม ชั้นระหว่างพื้นผิว 6 ถ้าความหนาแน่นแปรผกผันกับระยะห่างจากจุดกำเนิด ตัวเลือก ค้นหาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น 9 ค้นหาพื้นที่ผิวที่อยู่ภายในทรงกระบอก ค้นหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว ค้นหามวล ของวัตถุที่ล้อมรอบด้วยพาราโบลาและระนาบถ้าความหนาแน่นเท่ากับผลรวมของกำลังสองของพิกัดของจุด ตัวเลือก หาจุดศูนย์ถ่วงของรูปทรงแบนที่ล้อมรอบด้วยเส้น หาพื้นที่ผิวของกรวยด้านใน ทรงกระบอก จงหาปริมาตรของวัตถุที่ล้อมรอบด้วยพื้นผิว จงหามวลของวัตถุที่ถูกล้อมรอบด้วยส่วนร่วมที่มีลูกบอล 2 ลูก ถ้าความหนาแน่นเป็นสัดส่วนกับระยะห่างจากจุดถึงระนาบ O

44 สารบัญ การคำนวณปริพันธ์สองเท่าในพิกัดคาร์ทีเซียน การปริพันธ์สองเท่าในพิกัดเชิงขั้ว การใช้งานของปริพันธ์สองเท่า การคำนวณปริพันธ์สามในพิกัดคาร์ทีไซต์ การแทนที่ตัวแปรในปริพันธ์ตรี พิกัดทรงกระบอกและทรงกลม 7 6 การประยุกต์ใช้ตัวเลือกภาคผนวกของปริพันธ์สามส่วนสำหรับการบ้านส่วนบุคคล 7 ฉบับการศึกษา ปัญหาและแบบฝึกหัดจำนวนเต็มหลายตัว คำแนะนำเกี่ยวกับระเบียบวิธี รวบรวมโดย Olga Mikhailovna Karpilova บรรณาธิการ Yu N Litvinova การรวบรวม Yu N Litvinova ลงนามในการพิมพ์ รูปแบบ 6x/6 กระดาษออฟเซต การพิมพ์ออฟเซต เงื่อนไข l 7 การคัดลอกการหมุนเวียน สั่งซื้อศิลปะ S- 9/ Samara State Aerospace University 6 Samara Moskovskoe Highway สำนักพิมพ์ของมหาวิทยาลัยการบินและอวกาศ Samara State 6 ทางหลวง Samara Moskovskoe

Cos, sin, J dd dd d d 5 คำนวณ zdd zddz ddz โดยที่ด้านนอกของพื้นผิว z ตัดออกด้วยระนาบ z วิธีแก้ พื้นผิวเป็นรูปพาราโบลาที่นิยามไว้อย่างชัดเจนด้วยสมการ z ดังนั้น

สถาบันการศึกษาระดับอุดมศึกษาของรัฐ "มหาวิทยาลัยเบลารุส - รัสเซีย" ภาควิชาคณิตศาสตร์ขั้นสูง คณิตศาสตร์. คณิตศาสตร์ (บทพิเศษ) การวิเคราะห์ทางคณิตศาสตร์

คำแนะนำด้านระเบียบวิธีสำหรับงานคำนวณในหลักสูตรคณิตศาสตร์ขั้นสูง "สมการเชิงอนุพันธ์สามัญ ชุดปริพันธ์หลายตัว" ตอนที่ 3 หัวข้อ สารบัญปริพันธ์หลายตัว การคำนวณเลขสองและสาม

กระทรวงคมนาคมแห่งสหพันธรัฐรัสเซียสถาบันการศึกษางบประมาณของรัฐบาลกลางระดับอุดมศึกษา "มหาวิทยาลัยการขนส่งแห่งรัสเซีย (MIIT)" แผนก ITTSU ของ "อุดมศึกษาและคอมพิวเตอร์"

กระทรวงศึกษาธิการและวิทยาศาสตร์แห่งสหพันธรัฐรัสเซียสถาบันการศึกษางบประมาณของรัฐบาลกลางด้านการศึกษาวิชาชีพระดับสูง "มหาวิทยาลัยอุตสาหกรรมแห่งรัฐไซบีเรีย"

บทเรียนภาคปฏิบัติ 9 การคำนวณอินทิกรัลสองเท่าในพิกัดเชิงขั้ว การประยุกต์อินทิกรัลคู่ ลองพิจารณากรณีพิเศษของการเปลี่ยนแปลงตัวแปรที่มักใช้เมื่อคำนวณอินทิกรัลคู่

อินทิกรัลคู่ ตัวอย่างการแก้ปัญหา 1. ลดค่าอินทิกรัลคู่ f(x, y) dx dy ให้เหลือค่าที่ซ้ำกันในสองวิธี (ตามสูตร (1) และตามสูตร (2)) ถ้า G เป็นพื้นที่ที่ล้อมรอบด้วยเส้นโค้ง x = 1, y = x 2 , y =

การแสดงออกของมวลกายผ่านอินทิกรัลสามตัวในพิกัดทรงกระบอก คำจำกัดความและสูตรสำหรับการแก้ปัญหา คำจำกัดความ ลำแสงทรงกระบอกที่วางตามแนวแกน O รูปที่. เรียกว่าร่างกายที่ จำกัด G

กระทรวงศึกษาธิการแห่งสาธารณรัฐเบลารุส มหาวิทยาลัยเทคนิคแห่งชาติเบลารุส ภาควิชาวิศวกรรมศาสตร์ คณิตศาสตร์ N.A. คอนดราเทียวา โอ.จี. วิชเนฟสกายา เอ็น.เค. คู่มือระเบียบวิธีคณิตศาสตร์ Prikhach

คู่มือนี้มีไว้สำหรับนักศึกษานอกเวลาของ KSTU ในปีการศึกษาที่สอง คู่มือนี้ครอบคลุมหัวข้อต่อไปนี้ในรูปแบบที่กระชับและเข้าถึงได้: ปริพันธ์เชิงพหุคูณ ปริพันธ์เชิงโค้ง อนุกรม ทฤษฎีความน่าจะเป็น

กระทรวงวิทยาศาสตร์และการศึกษาของสหพันธรัฐรัสเซีย มหาวิทยาลัยมาตรวิทยาและการทำแผนที่แห่งรัฐมอสโก AV Aristarkhova, NG Babaeva การบ้านรายบุคคลในวิชาคณิตศาสตร์ขั้นสูง จำนวนเต็มหลายตัว

ธนาคารปัญหาในหัวข้อ “แคลคูลัสอินทิกรัล” * เปลี่ยนลำดับการรวม + d d * ค้นหาพื้นที่ของพื้นที่ราบที่ล้อมรอบด้วยเส้น =, =, = * คำนวณ (D) + acctg d โดยที่) +, + 9 , = (ภูมิภาค D,

กระทรวงวัฒนธรรมของสหพันธรัฐรัสเซีย สถาบันการศึกษางบประมาณสหพันธรัฐรัสเซีย สถาบันการศึกษาระดับอุดมศึกษาระดับมืออาชีพ เซนต์ปีเตอร์สเบิร์ก มหาวิทยาลัยภาพยนตร์และ

ส่วนหนึ่ง. ตัวอย่างข้อสอบวิชาคณิตศาสตร์ A. งานที่ง่ายที่สุดสำหรับสามคะแนน.. คำนวณอินทิกรัลอาร์กซิน e) ภาคเรียนที่ 2 ของ ISiA และ 9 กรัม i) 6 n j) 5 6 5 g) 6 d) cos h) z arcsin z. คำนวณอนุพันธ์

กระทรวงคมนาคมของสหพันธรัฐรัสเซียสถาบันการศึกษาด้านงบประมาณของสหพันธรัฐรัสเซียการศึกษาระดับอุดมศึกษา "มหาวิทยาลัยการขนส่งแห่งรัสเซีย (MIIT)" สถาบันเทคโนโลยีการขนส่ง

ภูมิภาค 3 (D) ในกรณีของเรา n คือเวกเตอร์ปกติของระนาบ XOY โดยที่ n k ( ) = ϕ, ϕ, จากนั้น = = และ n ( ) cos γ =, + + (ϕ) (ϕ) (ϕ) (ϕ) dq = + + dd หมายเหตุ หากพื้นผิว (Q) อยู่ในทิศทางที่ถูกต้อง

ปัญหาคณิตศาสตร์ (คณะเทคนิค ภาคเรียน) 7 ปริพันธ์ ค้นหาปริพันธ์ d d sin + d + + d + d + d 7 (+) d + + 8 d 9 cos d cos + d cos d + 8 d 9 d d + d 9 + d + 7 tg d 8 cosd เพราะบาป 9 วัน

การบรรยาย N 45 อินทิกรัลหลายตัวในพิกัดเชิงขั้ว ทรงกระบอก และทรงกลม การประยุกต์อินทิกรัลหลายตัวในพิกัดเชิงขั้ว อินทิกรัลสามตัวในพิกัดทรงกระบอกและทรงกลม

บท. อินทิกรัลหลายตัว.. บทเรียน... การลดอินทิกรัลสองเท่าให้เป็นอินทิกรัลซ้ำ เมื่อคำนวณอินทิกรัลคู่ ควรแยกสองกรณีออก () กรณีแรก ขอบเขตของการบูรณาการจะถูกจำกัดทางด้านซ้าย

วิทยาลัยการสื่อสารระดับสูง การรวบรวมการคำนวณมาตรฐานในสาขาวิชา "คณิตศาสตร์ขั้นสูง" ตอนที่ II สำหรับนักเรียนสาขาพิเศษ T 000 บริการไปรษณีย์มินสค์ 00 รวบรวมโดย Ryabenkova LA สิ่งพิมพ์ได้รับการอนุมัติในที่ประชุม

การบรรยาย เส้นลำดับที่สอง ไฮเปอร์โบลา ตัวอย่างเช่น เราจะค้นหาสมการที่กำหนดวงกลม พาราโบลา วงรี และวงกลม วงกลมคือเซตของจุดบนระนาบที่มีระยะห่างเท่ากันจากจุดที่กำหนด

สามอินทิกรัล Volchenko Yu.M. เนื้อหาบรรยาย แนวคิดเรื่องปริพันธ์สามประการ เงื่อนไขของการดำรงอยู่ของมัน ทฤษฎีบทค่าเฉลี่ย การคำนวณอินทิกรัลสามในพิกัดคาร์ทีเซียนและเส้นโค้ง ทริปเปิ้ล

LECTURE N. การคำนวณอินทิกรัลหลายตัว..การคำนวณอินทิกรัลสองเท่าในพิกัดคาร์ทีเซียนสี่เหลี่ยม.....การคำนวณอินทิกรัลคู่ (ขอบเขตตามอำเภอใจ)...อินทิกรัลสามตัว.....การคำนวณ

บทนำ แนวทางปฏิบัติประกอบด้วยการบ้าน 26 เวอร์ชันในหัวข้อ "เส้นตรงบนเครื่องบินและในอวกาศ" "เครื่องบิน" "เส้นโค้งและพื้นผิวลำดับที่สอง" ภายใต้รายบุคคล

สารบัญ บทนำ อินทิกรัลเชิงพหุคูณเส้นโค้งและพื้นผิว องค์ประกอบของทฤษฎีภาคสนาม ปัญหาสำหรับบทเรียนในชั้นเรียน ข้อมูลโดยย่อจากทฤษฎี ตัวอย่างการแก้ปัญหา ปัญหาสำหรับการทดสอบการเตรียมตนเอง

บทเรียนภาคปฏิบัติ 6 อินทิกรัลพื้นผิว 6 คำจำกัดความของคุณสมบัติ การคำนวณและการประยุกต์อินทิกรัลพื้นผิวประเภทที่ 6 คำจำกัดความของคุณสมบัติและการคำนวณอินทิกรัลพื้นผิวประเภทที่ 6 คำจำกัดความ

B. M. Mavrin, E. I. Balaev ภาพของ BODIES OF ROTATION Workshop Samara 2005 หน่วยงานของรัฐบาลกลางเพื่อการศึกษา สถาบันการศึกษาของรัฐของการศึกษาวิชาชีพชั้นสูง "SAMARSKY"

อินทิกรัลคู่ ปัญหาและแบบฝึกหัดสำหรับงานอิสระ 1. ลดปริพันธ์คู่ f(x, y) dx dy ให้เป็นอินทิกรัลซ้ำในสองวิธี ถ้า: G a) G เป็นรูปสามเหลี่ยมที่มีจุดยอด (1, 1), (4, 1 ), (4, 4); ข)

หน่วยงานกลางสำหรับการขนส่งทางรถไฟ Ural State Transport University ภาควิชาคณิตศาสตร์ขั้นสูง I N Pirogova เรขาคณิตเชิงวิเคราะห์ในตัวอย่างและปัญหา Yekaterinburg

บทที่ 1-2 อินทิกรัลจำกัดและการประยุกต์ I. ใช้สูตรนิวตัน-ไลบ์นิซ คำนวณอินทิกรัลจำกัดเขต: 1. (2 + 2) 2. / 3. (4.) 5. 6. 7. 8. Efimov-Pospelov 7.324-7.352, 7.380- 7.385,

การบรรยายครั้งที่ 7 อินทิกรัลที่ไม่เหมาะสม อินทิกรัลที่ไม่เหมาะสมคืออินทิกรัลจำกัดขอบเขตซึ่งเงื่อนไขอย่างน้อยหนึ่งเงื่อนไขสำหรับการมีอยู่ของอินทิกรัลจำกัด (เหมาะสม) ไม่เป็นที่พอใจ :) หรือ

บทเรียนที่ 14 ปริพันธ์สามเสื่อ การวิเคราะห์ประยุกต์ คณิตศาสตร์ ภาคการศึกษาที่ 3 การแก้ไข A1 ในอินทิกรัลถัดไป ไปที่พิกัดเชิงขั้วและจัดเรียงขีดจำกัดของอินทิเกรตทั้งสองลำดับ:

กระทรวงศึกษาธิการของสหพันธรัฐรัสเซีย มหาวิทยาลัยแห่งรัฐยาโรสลาฟล์ ตั้งชื่อตาม พี.จี. Demidova แผนกการวิเคราะห์แบบไม่ต่อเนื่องปัญหา PLANE และ LINE IN SPACE Yaroslavl รวบรวมโดยปริญญาเอก

MOSCOW AUTOMOBILE AND ROAD STATE TECHNICAL UNIVERSITY (MADI) INTEGRAL CALCULUS ตัวแปรของงานทดสอบหนังสือปัญหา MOSCOW AUTOMOBILE AND ROAD STATE TECHNICAL UNIVERSITY

หน่วยงานรัฐบาลกลางสำหรับการขนส่งทางรถไฟ มหาวิทยาลัยการขนส่งแห่งรัฐอูราล ภาควิชาคณิตศาสตร์ขั้นสูงและประยุกต์ P I Gnilomedov แอปพลิเคชันของจำนวนเต็มหลายตัวและเส้นโค้ง

กระทรวงศึกษาธิการและวิทยาศาสตร์ของสหพันธรัฐรัสเซียสถาบันการศึกษาอิสระแห่งรัฐสหพันธรัฐสถาบันการศึกษาระดับอุดมศึกษา "SAMARA STATE AEROSPACE UNIVERSITY ตั้งชื่อตาม

ภาคผนวก 5 กระทรวงเกษตรของสหพันธรัฐรัสเซียสถาบันการศึกษางบประมาณของรัฐบาลกลางระดับอุดมศึกษา "มหาวิทยาลัยเกษตรกรรมแห่งรัฐ Saratov"

องค์ประกอบของเรขาคณิตเชิงวิเคราะห์บนระนาบ เส้นตรง 1. คำนวณเส้นรอบรูปของสามเหลี่ยมที่มีจุดยอดคือ A(6; 7), B(3; 3), C(1; 5) 2. หาจุดที่ห่างจากจุด A(7;

กระทรวงศึกษาธิการและวิทยาศาสตร์แห่งสหพันธรัฐรัสเซีย มหาวิทยาลัยแห่งรัฐยาโรสลาฟล์ ตั้งชื่อตาม P. G. Demidova ภาควิชาพีชคณิตและตรรกะทางคณิตศาสตร์ เส้นโค้งลำดับที่สอง ตอนที่ 1 คำแนะนำเชิงระเบียบวิธี

สารบัญ ปริพันธ์หลายตัว แนวคิดของปริพันธ์คู่หลายตัว ขอบเขตบนระนาบ................. อินทิกรัลซ้ำ................. 3.3 การคำนวณอินทิกรัลคู่ในพิกัดคาร์ทีเซียน.. ...................

บทเรียนภาคปฏิบัติ 14 หัวข้อ: แผนพาราโบลา 1. ความหมายและสมการมาตรฐานของพาราโบลา สมบัติทางเรขาคณิตของพาราโบลา ตำแหน่งสัมพัทธ์ของพาราโบลาและเส้นที่ลากผ่านจุดศูนย์กลาง ขั้นพื้นฐาน

1 ปัญหาที่ง่ายที่สุดของเรขาคณิตวิเคราะห์บนระนาบ 11 ระยะห่างระหว่างจุดสองจุด พิจารณาระบบพิกัดสี่เหลี่ยม (คาร์ทีเซียน รูปที่ 1 จุดใดๆ M สอดคล้องกับพิกัด OA x

กระทรวงคมนาคมของสหพันธรัฐรัสเซียสถาบันการศึกษาของรัฐสหพันธรัฐการศึกษาวิชาชีพชั้นสูง ULYANOVSK โรงเรียนการบินระดับสูงของการบินพลเรือน (สถาบัน)

บทที่ 5 อินทิกรัลสามเท่า 5.1. ความหมายของอินทิกรัลสามตัว หลังจากแนะนำแนวคิดเรื่องอินทิกรัลสองเท่าในบทที่แล้ว มันจะเป็นธรรมดาที่จะดำเนินการสรุปเพิ่มเติมในปริภูมิสามมิติ

เส้นพีชคณิตบนระนาบ.. เส้นของลำดับแรก (เส้นบนระนาบ... ประเภทพื้นฐานของสมการของเส้นบนระนาบ เวกเตอร์ที่ไม่ใช่ศูนย์ n ตั้งฉากกับเส้นที่กำหนดเรียกว่าปกติ

กระทรวงศึกษาธิการและวิทยาศาสตร์ของสหพันธรัฐรัสเซีย มหาวิทยาลัยแห่งรัฐรัสเซียของน้ำมันและก๊าซตั้งชื่อตาม IMGUBKIN TS Filippova ANFILIPOV คำแนะนำด้านระเบียบวิธีสำหรับการศึกษาหัวข้อ "หลายรายการและเส้นโค้ง

Penza State Pedagogical University ตั้งชื่อตาม VGBelinsky OGNikitin ฟังก์ชั่นของตัวแปรแคลคูลัสหลายตัวแปร หนังสือเรียน Penza จัดพิมพ์โดยการตัดสินใจของกองบรรณาธิการและสำนักพิมพ์

หัวข้อ องค์ประกอบของเรขาคณิตวิเคราะห์บนระนาบและในอวกาศ การบรรยาย.. เส้นตรงบนระนาบ แผน วิธีพิกัดบนระนาบ.. เส้นตรงในพิกัดคาร์ทีเซียน.. เงื่อนไขความขนานและความตั้งฉาก

มหาวิทยาลัยเทคนิคแห่งรัฐมอสโกตั้งชื่อตาม N.E. บาวแมน คณะวิทยาศาสตร์พื้นฐาน ภาควิชาคณิตศาสตร์แบบจำลอง A.N. Kaviakovykov, A.P. เครเมนโก

บทที่ 5 อินทิกรัลพื้นผิวประเภทที่ 3 (ต่อ) 5 ปัญหาในชั้นเรียน ปัญหาที่ 5 (4349) คำนวณอินทิกรัลโดยที่ส่วนหนึ่งของพื้นผิวของกรวย z d, x = ρ cos ϕ sin α, y = ρ sin ϕ sin α, z = ρ cos α (( ρh,

หน่วยงานกลางเพื่อการศึกษา มหาวิทยาลัยป่าไม้รัฐอูราล ภาควิชาความแข็งแกร่งของวัสดุและกลศาสตร์เชิงทฤษฎี V. A. Kalentyev V. M. Kalinin L. T. Raevskaya N. I. Chashchin

องค์ประกอบของการจัดหมวดหมู่เรขาคณิตวิเคราะห์ของระนาบในพื้นที่สามมิติ เขียนสมการเวกเตอร์ของระนาบและอธิบายความหมายของปริมาณที่รวมอยู่ในสมการนี้ เขียนสมการทั่วไปของระนาบ

3 ตัวอย่าง เขียนนิพจน์สำหรับโมเมนต์คงที่ของบริเวณวัสดุแบน (D) ตามสูตร (3) โดยคำนึงถึงรูป (Φ) เรามี: ρ, dd, ρ, dd ขึ้นอยู่กับความหมายเชิงกลของโมเมนต์คงที่

ปัญหาที่ 1 ค้นหาพิกัดของจุดศูนย์ถ่วงของครึ่งวงกลม y = r 2 x 2 ปัญหาที่ 5 พื้นที่ของส่วนหนึ่งของพื้นผิว z = 1 4 xy ที่อยู่ภายในพื้นผิว x 2 + y 2 = 16 ปัญหา 2 เปลี่ยนลำดับการรวมระบบ

กระทรวงศึกษาธิการและวิทยาศาสตร์ของยูเครน สถาบันโลหะวิทยาแห่งชาติของยูเครน คำแนะนำด้านระเบียบวิธีวิทยาสำหรับการแก้ปัญหาในสาขาวิชาคณิตศาสตร์ที่สูงขึ้นและตัวเลือกการทดสอบภาคปฏิบัติ

บทเรียนเชิงปฏิบัติในหลักสูตรคณิตศาสตร์ระดับสูง (ภาคเรียนที่ 3) ตามหนังสือเรียน "การรวบรวมการมอบหมายงานรายบุคคลในคณิตศาสตร์ขั้นสูง" เล่มที่ 3 เอ็ด Ryabushko A.P. สำหรับนักศึกษาเต็มเวลา

มหาวิทยาลัยเทคนิคแห่งรัฐมอสโกตั้งชื่อตาม N.E. บาวแมน คณะวิทยาศาสตร์พื้นฐาน ภาควิชาคณิตศาสตร์คอมพิวเตอร์และฟิสิกส์คณิตศาสตร์ A.I. Levin MULTIPLE INTEGRALS อิเล็กทรอนิกส์

แคลคูลัสอินทิกรัลของฟังก์ชันของตัวแปรหลายตัวของเส้นโค้งสองเท่าสามเท่าตามความยาวส่วนโค้ง (ชนิดแรก) พื้นผิวเทียบกับพื้นที่ผิว (ชนิดแรก) ให้นิยามฟังก์ชัน f()

1.3. บทที่ 3 1.3.1. การคำนวณอินทิกรัลสามตัวในพิกัดคาร์ทีเซียน อนุญาต เป็นโดเมนเชิงพื้นที่ D การฉายภาพบนระนาบ Oxy ขอบเขตเรียกว่า -regular ถ้ามีเส้นแนวตั้ง

กระทรวงศึกษาธิการของสาธารณรัฐเบลารุส มหาวิทยาลัยเทคนิคแห่งชาติเบลารุส ภาควิชาวิศวกรรมศาสตร์ คณิตศาสตร์ คณิตศาสตร์ชั้นสูง คู่มือการแก้ปัญหาสำหรับนักศึกษาวิศวกรรมเครื่องกลและเทคโนโลยี

บทเรียนภาคปฏิบัติ 1 หัวข้อ: แผนไฮเปอร์โบลา 1 ความหมายและสมการทางบัญญัติของไฮเปอร์โบลา คุณสมบัติทางเรขาคณิตของไฮเปอร์โบลา ตำแหน่งสัมพัทธ์ของไฮเปอร์โบลาและเส้นที่ลากผ่านจุดศูนย์กลางของมัน เส้นกำกับ

Def . อนุญาต ,
,

.

เซตหนึ่งเรียกว่าช่วงปิดหรือแถบปิดเข้ามา .

เซตนี้เรียกว่าช่วงเปิด

หรือลำแสงเปิดเข้ามา .

Def . การวัดช่วงเวลา และ ปริมาณเรียกว่า:

(อย่างแม่นยำมากขึ้น
).

Def . ถ้า
ดังนั้น
แล้วช่วงเวลา เรียกว่าเสื่อมทรามและ
.

คุณสมบัติของการวัดช่องว่าง:

ก) คิดบวก:
, และ
แล้วและเมื่อเท่านั้น – เสื่อมสภาพ

ข) ความสม่ำเสมอเชิงบวก: .

วี) สารเติมแต่ง:

* สำหรับ
ดังนั้น
;

* สำหรับ
และ

.

ช) ความซ้ำซากจำเจของการวัด: .

Def . เส้นผ่านศูนย์กลางของลำแสง (ช่องว่าง) คือค่า:

โปรดทราบว่า
และ
– นี่ไม่ใช่เรื่องเดียวกัน ตัวอย่างเช่น ถ้า – เสื่อมแล้ว
,ก
(พูด, พูดแบบทั่วไป, พูดทั่วๆไป).

โดยที่: * ;

* ;*
.

Def . จำนวนทั้งสิ้น
ช่วงย่อยของช่วงเวลา เรียกว่าพาร์ติชันช่วงเวลา , ถ้า: *;

*
; *
; *
; *
.

ขนาด
เรียกว่าพารามิเตอร์พาร์ติชัน ป(ซึ่ง
).

Def . แยก เรียกว่าการปรับแต่งพาร์ติชัน ถ้าองค์ประกอบทั้งหมดของพาร์ติชัน ได้รับจากการแบ่งพาร์ติชันองค์ประกอบพาร์ติชัน .

ระบุโดย:
. อ่าน: เล็กกว่า หรือ ใหญ่กว่า .

สำหรับอัตราส่วน “มาก-น้อย” จะเป็นดังนี้:

*. การขนส่ง – ; *.
;

*.


; *.

|
.

§. คำจำกัดความของอินทิกรัลหลายตัว

อนุญาต
– ไม้ (ช่องว่าง) ใน ,
– การแบ่งช่องว่าง ฉัน. ในแต่ละช่วงของพาร์ติชั่น ทำเครื่องหมายจุด
.

เราได้รับ
พาร์ทิชันที่มีจุดทำเครื่องหมายสำหรับ
.

ขนาด
เรียกว่าผลรวมอินทิกรัลรีมันน์ของฟังก์ชัน ฉ (x) ในช่วงเวลา ฉัน โดยฉากกั้นที่มีจุดทำเครื่องหมายไว้
.

Def :
=
=
.

การกำหนด – ฟังก์ชั่นมากมายรวมอยู่ในลำแสง ฉัน มาเขียนกัน:

Def : ε > 0 δ>0<.

ถ้าสำหรับฟังก์ชั่น ฉ(x) บน ฉันและพาร์ติชั่น
- แสดงโดย
– ค่าที่ใหญ่ที่สุดและน้อยที่สุดของฟังก์ชัน ฉ(x) บน ฉัน เคแล้วค่าต่างๆ
=
และ
=
เรียกว่าผลรวมดาร์บูซ์ล่างและบน

§. เกณฑ์ดาร์โบซ์สำหรับการมีอยู่ของอินทิกรัลหลายตัว.

ต 0 . เพื่อการทำงาน
ถูกรวมเข้ากับลำแสง (เหล่านั้น.
) มีความจำเป็นและเพียงพอเช่นนั้น

. Δ▲.

การรวมฟังก์ชันบนลำแสงในปริภูมิแบบยุคลิดถูกกำหนดไว้ เราจะรวมฟังก์ชันเข้ากับชุดที่มีขอบเขตโดยพลการจากปริภูมิแบบยุคลิดได้อย่างไร

ให้เรานิยามอินทิกรัลของฟังก์ชัน ฉ โดยหลาย ๆ คน
.

Def : อนุญาต
และ
– จำกัด เช่น
. การทำงาน
เราเรียกฟังก์ชันเฉพาะของเซต ม.

แล้ว:
≡
.

คำจำกัดความของอินทิกรัลชุดไม่ได้ขึ้นอยู่กับลำแสงที่มี มเลือกไว้เช่น

.

ซึ่งหมายความว่านิยามของอินทิกรัลเหนือเซตนั้นถูกต้อง

เงื่อนไขที่จำเป็นสำหรับการบูรณาการเพื่อการทำงาน ฉ(x) บน มสามารถบูรณาการได้ก็เป็นสิ่งจำเป็น ฉ(x) จำกัดอยู่เพียง ม. Δ▲.

§. คุณสมบัติของอินทิกรัลหลายตัว

1  . ความเป็นเส้นตรง: มากมาย ร มฟังก์ชั่นที่บูรณาการได้ในชุด เอ็ม –เชิงเส้น

พื้นที่และ
– ฟังก์ชันเชิงเส้น

2  . เงื่อนไขการทำให้เป็นมาตรฐาน:
. ทางเข้าอีกรูปแบบหนึ่ง
โดยพื้นฐานแล้วจะกำหนดหน่วยวัดของเซตตามอำเภอใจจากปริภูมิแบบยุคลิด

3  . หากมีอินทิกรัลบนเซตของศูนย์การวัด Lebesgue แสดงว่ามีค่าศูนย์นั้น

เท่ากับศูนย์

บันทึก:พวงของ มเรียกว่าเซตของเลอเบสเกจวัดศูนย์

ถ้า

ดังนั้น
และ
.

4  . ก.;ข.;

วี.ถ้า
และ – แยกจากศูนย์ด้วย ม, ที่

5  .
และ ฉ=กพีวี (เกือบทุกที่) บน ม, ที่
.

6  . สารเติมแต่ง: ถ้า
และ
ที่

,

โดยทั่วไป:
.

Δ มันตามมาจากความเท่าเทียมกัน: ▲

7  . โมโนโทน:
และ
ที่
.

8  . การบูรณาการความไม่เท่าเทียมกัน: ถ้า
อิโต้

.

9  . อนุญาต


. เพื่อที่จะ
จึงมีความจำเป็นและเพียงพอที่จะมีจุดภายในชุด มในที่นั้น ฉ (x) > 0 และต่อเนื่อง

10  . บูรณาการของโมดูลฟังก์ชันบูรณาการ:
.

11  . ทฤษฎีบทค่าเฉลี่ย:
,
บน มรักษาเครื่องหมายและ
, ที่

.

ถ้าเป็นชุด ม– สอดคล้องกันและ ฉ(x) – เปิดต่อเนื่อง
ที่
ดังนั้น
.

12  . เพื่อให้อินทิกรัลของฟังก์ชันไม่เป็นลบเท่ากับ 0

จำเป็นและเพียงพอต่อการ ฉ(x) = 0 เกือบทุกที่ ม.

13  . ทฤษฎีบทของฟูบินีสำหรับอินทิกรัลสองเท่า:

ให้พื้นที่
- สี่เหลี่ยมผืนผ้า:. จากนั้น หากมีอินทิกรัลเดี่ยวภายในอยู่ เพื่อค้นหาอินทิกรัลคู่ คุณสามารถดำเนินการอินทิกรัลซ้ำได้ (ดูรูปที่ a):

, หรือ

อี

หากขอบเขตของการอินทิเกรตไม่ใช่สี่เหลี่ยม ทฤษฎีบทของ Fubini ยังคงใช้ได้และมีรูปแบบ (ดูรูปที่ b):
. (*)

บันทึก:ขีดจำกัดภายนอกของการรวมระบบจะต้องคงที่ ขีดจำกัดภายในของการรวมระบบอาจขึ้นอยู่กับตัวแปรที่ยังไม่ได้ดำเนินการรวมระบบ

สามารถรับสูตร (*) ได้โดยใช้ฟังก์ชันลักษณะเฉพาะที่กำหนด ดี.

สำหรับอินทิกรัลหลายรายการ:

อนุญาตและเซตย่อยบางส่วนของปริภูมิแบบยุคลิด และ . ขอให้เรานิยามผลคูณคาร์ทีเซียนของเซตเหล่านี้ ซึ่งเป็นเซตย่อยของปริภูมิแบบยุคลิด
:.

แล้วทฤษฎีบทของฟูบินีสำหรับ
มีรูปแบบ:
.

ทฤษฎีบทนี้ใช้ได้กับคานเช่นกัน เอ็กซ์และ ยและสำหรับการกำหนดค่าที่ซับซ้อนมากขึ้น

ตัวอย่าง:

1 0 . คำนวณ
ถ้าเป็นเขตแดนของพื้นที่
กำหนดโดยสมการ:

. เมื่อค้นหาจุดตัดกันของเส้นโค้งที่กำหนดขอบเขตของพื้นที่ เราจะได้จุดสองจุด:
และ
. จากนั้นการจัดเตรียมขีดจำกัดการรวมที่เป็นไปได้เมื่อผ่านไปยังอินทิกรัลแบบวนซ้ำจะให้:

ก)
;

2

0 . เปลี่ยนลำดับการรวมในอินทิกรัลแบบวนซ้ำ:
.

–

.

สูตรอาหาร:เมื่อตั้งค่าขีดจำกัดการรวมในอินทิกรัลคู่ ขอแนะนำให้เริ่มต้นด้วยขีดจำกัดการรวมภายนอก

3

0 . คำนวณ:
, ถ้า

การส่งผ่านไปยังอินทิกรัลแบบวนซ้ำจะให้:
.

ในเวลาเดียวกัน ในอินทิกรัลสามตัว การวางขีดจำกัดจะต้องเริ่มต้นด้วยขีดจำกัดภายในของการอินทิเกรต จากนั้นจึงจัดโครงการพื้นที่ วีไปที่เครื่องบิน xOy

กำหนดขอบเขตในพื้นที่ ดี– นอนอยู่บนเครื่องบิน xOy.

4 0 . เปลี่ยนลำดับการรวมในอินทิกรัลแบบวนซ้ำ:
.

อินทิกรัลหลายรายการ

อินทิกรัลของฟังก์ชันที่ระบุในบางพื้นที่บนระนาบสามมิติหรือ n-พื้นที่มิติ ท่ามกลางเคและ แยกความแตกต่างระหว่างอินทิกรัลคู่, อินทิกรัลสาม ฯลฯ n- อินทิกรัลหลายรายการ

ให้ฟังก์ชัน ฉ(เอ็กซ์, ย) มีให้ในบางพื้นที่ ดีเครื่องบิน xOy.มาแบ่งพื้นที่กัน ดีบน nพื้นที่บางส่วน ฉันซึ่งมีพื้นที่เท่ากัน ฉันเลือกในแต่ละพื้นที่ ฉันจุด ( ξi, ηi) (ซม. ข้าว. ) และเขียนผลรวมอินทิกรัล

หากมีการลดขนาดเส้นผ่านศูนย์กลางสูงสุดของพื้นที่บางส่วนได้ไม่จำกัด ฉันจำนวนเงิน สมีขีดจำกัดโดยไม่คำนึงถึงการเลือกคะแนน ( ξi, ηi) จากนั้นลิมิตนี้เรียกว่าอินทิกรัลสองเท่าของฟังก์ชัน ฉ(เอ็กซ์, ย) ตามภูมิภาค ดีและแสดงถึง

อินทิกรัลสามถูกกำหนดในทำนองเดียวกัน และโดยทั่วไป n- อินทิกรัลหลายรายการ

สำหรับการมีอยู่ของอินทิกรัลคู่ ก็เพียงพอแล้ว เช่น บริเวณนั้น ดีเป็นขอบเขตกำลังสองแบบปิด (ดูบริเวณกำลังสอง) และฟังก์ชัน ฉ(เอ็กซ์, ย) ต่อเนื่องกัน ดี.เคและ. มีคุณสมบัติหลายประการคล้ายกับคุณสมบัติของปริพันธ์อย่างง่าย . เพื่อคำนวณเคและ มักจะนำไปสู่อินทิกรัลแบบวนซ้ำ (ดูอินทิกรัลแบบวนซ้ำ) ในกรณีพิเศษสำหรับข้อมูลของ K. และ สูตรของกรีนและสูตรของออสโตรกราดสกีสามารถใช้เป็นอินทิกรัลของมิติที่ต่ำกว่าได้ เคและ. มีการใช้งานที่หลากหลาย: ใช้เพื่อแสดงปริมาตรของร่างกาย มวล โมเมนต์คงที่ โมเมนต์ความเฉื่อย ฯลฯ

สารานุกรมผู้ยิ่งใหญ่แห่งสหภาพโซเวียต - ม.: สารานุกรมโซเวียต. 1969-1978 .

ดูว่า "อินทิกรัลหลายรายการ" ในพจนานุกรมอื่น ๆ คืออะไร:

อินทิกรัลของฟังก์ชันของตัวแปรหลายตัว คำนวณโดยใช้ผลรวมอินทิกรัล คล้ายกับอินทิกรัลชี้ขาดของฟังก์ชันของตัวแปรตัวหนึ่ง (ดูแคลคูลัสอินทิกรัล) ขึ้นอยู่กับจำนวนตัวแปร มี double, triple, n... ... พจนานุกรมสารานุกรมขนาดใหญ่

อินทิกรัลจำกัดจำนวนฟังก์ชันของตัวแปรหลายตัว มีแนวคิดที่หลากหลายของเคและ (อินทิกรัลรีมันน์, อินทิกรัลเลอเบส, อินทิกรัลเลอเบส สตีลเยส ฯลฯ) อินทิกรัลรีมันน์หลายตัวถูกนำมาใช้บนพื้นฐานของการวัดของจอร์แดน ให้ E เป็นค่าของจอร์แดนที่วัดได้... ... สารานุกรมคณิตศาสตร์

ในการวิเคราะห์ทางคณิตศาสตร์ อินทิกรัลหลายตัวหรือหลายตัวคือชุดของอินทิกรัลที่นำมาจากตัวแปร ตัวอย่างเช่น หมายเหตุ: อินทิกรัลหลายตัวเป็นอินทิกรัลจำกัด การคำนวณจะให้ผลลัพธ์เป็นตัวเลขเสมอ สารบัญ 1... ...วิกิพีเดีย

อินทิกรัลของฟังก์ชันของตัวแปรหลายตัว คำนวณโดยใช้ผลรวมอินทิกรัล คล้ายกับอินทิกรัลชี้ขาดของฟังก์ชันของตัวแปรตัวหนึ่ง (ดูแคลคูลัสอินทิกรัล) ขึ้นอยู่กับจำนวนตัวแปร มี double, triple, n... ... พจนานุกรมสารานุกรม

อินทิกรัลของฟังก์ชันของตัวแปรหลายตัว กำหนดโดยใช้ผลรวมปริพันธ์ซึ่งมีการกำหนดในทำนองเดียวกัน อินทิกรัลของฟังก์ชันของตัวแปรตัวเดียว (ดูแคลคูลัสอินทิกรัล) ขึ้นอยู่กับจำนวนตัวแปร มีสองเท่า สามเท่า ฉัน... ... วิทยาศาสตร์ธรรมชาติ. พจนานุกรมสารานุกรม

หมายเหตุ: ทุกแห่งในบทความนี้ที่ใช้เครื่องหมาย จะต้องหมายถึงอินทิกรัลรีมันน์ (หลายรายการ) เว้นแต่จะระบุไว้เป็นอย่างอื่น ทุกที่ในบทความนี้ที่เราพูดถึงความสามารถในการวัดของเซต เราหมายถึงความสามารถในการวัดของจอร์แดน ถ้าไม่ใช่... ... Wikipedia

อินทิกรัลพหุคูณของรูปแบบ โดยที่ ซึ่งเป็นค่าเฉลี่ยของระดับ 2k ของโมดูลัสของผลรวมตรีโกณมิติ ทฤษฎีบทของวิโนกราดอฟเกี่ยวกับค่าของอินทิกรัลซึ่งเป็นทฤษฎีบทค่าเฉลี่ย เป็นพื้นฐานของการประมาณค่าของผลรวมไวล์ วรรณกรรม Vinogradova inte... Wikipedia

อินทิกรัลจำกัดความเป็นพื้นที่ของรูป คำนี้มีความหมายอื่น ดูอินทิกรัล (ความหมาย) อินทิกรัลของฟังก์ชัน ... Wikipedia

อินทิกรัลที่ดำเนินการอินทิเกรตบนตัวแปรต่างๆ ตามลำดับ กล่าวคือ อินทิกรัลของรูปแบบ (1) ฟังก์ชัน f(x, y) ถูกกำหนดบนเซต A ที่อยู่ในผลคูณโดยตรง XX Y ของช่องว่าง X และ Y โดยที่ s ได้รับการวัดอันจำกัด mx และ my,… … สารานุกรมคณิตศาสตร์

อินทิกรัลที่ถ่ายตามเส้นโค้งใดๆ บนเครื่องบินหรือในอวกาศ มีเคและ. ประเภทที่ 1 และ 2 เคและ. ตัวอย่างเช่น ประเภทที่ 1 เกิดขึ้นเมื่อพิจารณาปัญหาในการคำนวณมวลของเส้นโค้งความหนาแน่นแปรผัน ถูกกำหนดไว้แล้ว...... สารานุกรมผู้ยิ่งใหญ่แห่งสหภาพโซเวียต

เรามาดูรายละเอียดเกี่ยวกับงานของ Ostrogradsky เกี่ยวกับอินทิกรัลหลายตัวกันดีกว่า

สูตรของออสโตรกราดสกีในการแปลงอินทิกรัลสามให้เป็นอินทิกรัลคู่ ซึ่งเรามักจะเขียนอยู่ในรูป

โดยที่ div A คือความแตกต่างของสนามของเวกเตอร์ A

Аn คือผลคูณสเกลาร์ของเวกเตอร์ A และเวกเตอร์หน่วยของเส้นปกติภายนอก n ของพื้นผิวขอบเขต ในวรรณกรรมทางคณิตศาสตร์ ก่อนหน้านี้มักเกี่ยวข้องกับชื่อของเกาส์และกรีน

อันที่จริง ในงานของเกาส์เกี่ยวกับการดึงดูดของทรงกลม เราสามารถเห็นเฉพาะกรณีพิเศษของสูตร (1) เท่านั้น เช่น ด้วย P=x, Q=R=0 เป็นต้น สำหรับเจ. กรีนในงานของเขา ในทฤษฎีไฟฟ้าและไม่มีแม่เหล็กเลยในสูตร (1) มันได้รับความสัมพันธ์อีกอย่างหนึ่งระหว่างปริพันธ์สามและสองเท่า กล่าวคือ สูตรของกรีนสำหรับตัวดำเนินการลาปลาซ ซึ่งสามารถเขียนได้ในรูปแบบ

แน่นอน เราสามารถหาสูตร (1) จาก (2) ได้ โดยสมมติว่า

และในทำนองเดียวกันก็เป็นไปได้ที่จะได้สูตร (2) จากสูตร (1) แต่กรีนไม่คิดจะทำสิ่งนี้

โดยทางด้านซ้ายคืออินทิกรัลเหนือปริมาตร และทางขวาคืออินทิกรัลเหนือพื้นผิวขอบเขต และนี่คือโคไซน์ทิศทางของเส้นปกติภายนอก

ต้นฉบับปารีสของ Ostrogradsky เป็นพยานด้วยความมั่นใจอย่างสมบูรณ์ว่าทั้งการค้นพบและข้อความแรกของทฤษฎีบทอินทิกรัล (1) เป็นของเขา ได้มีการระบุและพิสูจน์เป็นครั้งแรกเหมือนกับที่กำลังทำอยู่นี้ใน “การพิสูจน์ทฤษฎีบทของแคลคูลัสอินทิกรัล” นำเสนอต่อ Paris Academy of Sciences เมื่อวันที่ 13 กุมภาพันธ์ พ.ศ. 2369 หลังจากนั้นจึงได้มีการจัดทำสูตรอีกครั้งในส่วนนั้นของ “ บันทึกความทรงจำเกี่ยวกับการแพร่กระจายความร้อนในของแข็ง”” ซึ่ง Ostrogradsky นำเสนอเมื่อวันที่ 6 สิงหาคม พ.ศ. 2370 “ บันทึกช่วยจำ” ได้รับการมอบให้เพื่อตรวจสอบฟูริเยร์และปัวซองและคนหลังอ่านอย่างแน่นอนตามหลักฐานจากรายการในครั้งแรก หน้าต้นฉบับทั้งสองส่วน แน่นอนว่าความคิดในการอ้างถึงทฤษฎีบทนั้นซึ่งเขาคุ้นเคยในงานของ Ostrogradsky เมื่อสองปีก่อนจะนำเสนอผลงานของเขาเกี่ยวกับทฤษฎีบทความยืดหยุ่นนั้นไม่ได้เกิดขึ้นกับปัวซองด้วยซ้ำ

สำหรับความสัมพันธ์ระหว่างงานเกี่ยวกับอินทิกรัลหลายตัวของ Ostrogradsky และ Green เราจำได้ว่าใน "หมายเหตุเกี่ยวกับทฤษฎีความร้อน" ได้สูตรมาซึ่งรวมเอาสูตรของ Green เองเป็นกรณีพิเศษมาก สัญลักษณ์ Cauchy ที่ผิดปกติซึ่งใช้โดย Ostrogradsky ใน "บันทึก" จนกระทั่งเมื่อไม่นานมานี้ได้ซ่อนการค้นพบที่สำคัญนี้จากนักวิจัย แน่นอนว่า Greene ยังคงได้รับเกียรติจากการค้นพบและการตีพิมพ์ครั้งแรกในปี 1828 ของสูตรสำหรับตัวดำเนินการ Laplace ที่ใช้ชื่อของเขา

การค้นพบสูตรสำหรับการแปลงอินทิกรัลสามตัวให้เป็นอินทิกรัลสองเท่าช่วยให้ออสโตรกราดสกีแก้ปัญหาการเปลี่ยนแปลงอินทิกรัล n-fold กล่าวคือ ได้สูตรทั่วไปสำหรับการแปลงอินทิกรัลจากการแสดงออกของประเภทของความแตกต่างเหนือ n- โดเมนมิติและอินทิกรัลเหนือพื้นผิวเหนือ S ซึ่งล้อมรอบด้วยสมการ L(x,y, z,…)=0 หากเรายึดถือสัญกรณ์ก่อนหน้า สูตรจะมีรูปแบบ

อย่างไรก็ตาม Ostrogradsky ไม่ได้ใช้ภาพเรขาคณิตและคำศัพท์ที่เราใช้: เรขาคณิตของช่องว่างหลายมิติยังไม่มีอยู่ในเวลานั้น

ใน “บันทึกความทรงจำเกี่ยวกับแคลคูลัสของการแปรผันของอินทิกรัลหลายตัว” มีการพิจารณาประเด็นที่สำคัญอีกสองประเด็นในทฤษฎีอินทิกรัลดังกล่าว ประการแรก Ostrogradsky ได้มาจากสูตรสำหรับการเปลี่ยนตัวแปรในอินทิกรัลหลายมิติ ประการที่สอง เป็นครั้งแรกที่เขาให้คำอธิบายที่สมบูรณ์และแม่นยำเกี่ยวกับวิธีการคำนวณอินทิกรัล n-fold โดยใช้การอินทิเกรตต่อเนื่องกัน n ครั้งเหนือตัวแปรแต่ละตัวภายในขีดจำกัดที่เหมาะสม สุดท้ายนี้ จากสูตรที่มีอยู่ในบันทึกนี้ กฎทั่วไปของการสร้างความแตกต่างด้วยความเคารพต่อพารามิเตอร์ของอินทิกรัลหลายมิตินั้นได้มาอย่างง่ายดาย เมื่อไม่เพียงแต่ฟังก์ชันอินทิแกรนด์เท่านั้น แต่ยังรวมถึงขอบเขตของโดเมนอินทิกรัลด้วยที่ขึ้นอยู่กับพารามิเตอร์นี้ด้วย กฎที่มีชื่อนั้นต่อจากสูตรในบันทึกความทรงจำในลักษณะธรรมชาติที่นักคณิตศาสตร์รุ่นหลังระบุด้วยสูตรหนึ่งของบันทึกความทรงจำนี้ด้วยซ้ำ

Ostrogradsky ทุ่มเทงานพิเศษในการเปลี่ยนแปลงตัวแปรในอินทิกรัลหลายตัว สำหรับอินทิกรัลคู่ ออยเลอร์ได้กฎที่สอดคล้องกันโดยใช้การแปลงแบบเป็นทางการ สำหรับอินทิกรัลสามตัว ลากรองจ์ได้มาจากกฎนั้น อย่างไรก็ตาม แม้ว่าผลลัพธ์ของลากรองจ์จะถูกต้อง แต่การให้เหตุผลของเขาไม่ถูกต้อง ดูเหมือนว่าเขาจะดำเนินการต่อจากข้อเท็จจริงที่ว่าองค์ประกอบของปริมาตรในตัวแปรเก่าและใหม่ในพิกัด - มีค่าเท่ากัน Ostrogradsky ทำผิดพลาดที่คล้ายกันตั้งแต่เริ่มต้นในการอ้างถึงกฎสำหรับการแทนที่ตัวแปร ในบทความเรื่องการแปลงตัวแปรในปริพันธ์หลายรายการ Ostrogradsky เปิดเผยข้อผิดพลาดของ Lagrange และเป็นครั้งแรกที่สรุปวิธีการทางเรขาคณิตเชิงภาพสำหรับการแปลงตัวแปรในปริพันธ์คู่ซึ่งในรูปแบบที่เข้มงวดกว่าเล็กน้อยก็ถูกนำเสนอเช่นกัน ในคู่มือของเรา กล่าวคือ เมื่อแทนที่ตัวแปรในอินทิกรัลโดยใช้สูตร โดเมนการรวมจะถูกหารด้วยเส้นพิกัดของสองระบบ u=const, v=const ลงในรูปสี่เหลี่ยมเส้นโค้งที่เล็กที่สุด จากนั้นหาอินทิกรัลได้โดยการบวกองค์ประกอบเหล่านั้นที่ตรงกับแถบโค้งที่แคบอย่างไม่สิ้นสุดก่อน จากนั้นจึงรวมองค์ประกอบต่างๆ เข้าด้วยกันเป็นแถบจนกว่าองค์ประกอบทั้งหมดจะหมด การคำนวณอย่างง่ายจะให้พื้นที่ซึ่งสามารถพิจารณาเป็นรูปสี่เหลี่ยมด้านขนานได้ โดยนิพจน์นั้นจะถูกเลือกเพื่อให้พื้นที่นั้นเป็นค่าบวก ผลลัพธ์ที่ได้คือสูตรอันโด่งดัง

สำหรับฟังก์ชันของตัวแปรสองตัวที่ระบุเป็น z = ฉ(x, ย) .

อินทิกรัลคู่เขียนได้ดังนี้:

ที่นี่ ดี– รูปแบนที่ล้อมรอบด้วยเส้น ซึ่งเป็นนิพจน์ที่ให้ (ความเท่าเทียมกัน) ในการคำนวณอินทิกรัลคู่ ซ้ายและขวาคือความเท่าเทียมกันซึ่งมีตัวแปรทางด้านซ้ายเป็น xและด้านบนและด้านล่าง – ตามความเท่าเทียมกันซึ่งมีตัวแปรทางด้านซ้ายเป็น ย. สถานที่แห่งนี้ยังคงเป็นหนึ่งในจุดที่สำคัญที่สุดสำหรับการทำความเข้าใจเทคนิคการคำนวณอินทิกรัลสองเท่า

คำนวณอินทิกรัลสองเท่า - หมายถึงการหาจำนวนเท่ากับพื้นที่ของรูปดังกล่าว ดี .

จนกว่าเราจะได้สัมผัส คำจำกัดความอินทิกรัลสองเท่า และเราจะเรียนรู้การคำนวณมัน จะเข้าใจได้ง่ายขึ้นว่าอินทิกรัลสองเท่าคืออะไรเมื่อคุณแก้ไขปัญหาต่างๆ เพื่อคำนวณหาได้ ดังนั้นคุณจะพบคำจำกัดความของอินทิกรัลคู่ในตอนท้ายของบทเรียนนี้ เมื่อมองไปข้างหน้าเล็กน้อย เราจะสังเกตได้เพียงว่าคำจำกัดความของอินทิกรัลสองเท่านั้นสัมพันธ์กับตัวเลขที่กล่าวมาด้วย ดี .

ถ้าเป็นรูป ดีเป็นรูปสี่เหลี่ยมผืนผ้า เส้นทุกเส้นที่กั้นไว้เป็นเส้นตรง ถ้าเป็นรูป ดี- เป็นเส้นโค้ง จากนั้นด้านซ้ายและขวาจะถูกจำกัดด้วยเส้นตรง และด้านบนและด้านล่างด้วยเส้นโค้ง ซึ่งกำหนดโดยความเท่าเทียมกันที่ได้รับในงาน นอกจากนี้ยังมีกรณีที่มีรูปร่าง ดี- รูปสามเหลี่ยม แต่เพิ่มเติมในกรณีเช่นนี้ให้ไกลออกไปอีกเล็กน้อย

ในการคำนวณอินทิกรัลสองเท่า จึงจำเป็นต้องจัดเรียงเส้นที่อยู่ติดกับรูป ดีซึ่งมีชื่อที่เข้มงวด - ภูมิภาคแห่งการรวมกลุ่ม เรียงไปทางซ้ายและขวาและบนและล่าง ซึ่งจะต้องใช้เมื่อใด ลดอินทิกรัลสองเท่าให้เป็นอินทิกรัลแบบวนซ้ำ – วิธีการคำนวณอินทิกรัลสองเท่า

กรณีพื้นที่สี่เหลี่ยม:

กรณีของบริเวณโค้ง:

และนี่คือคำตอบของอินทิกรัลจำกัดขอบเขตที่คุ้นเคยอยู่แล้ว โดยให้ขีดจำกัดบนและล่างของอินทิเกรตไว้ นิพจน์ที่กำหนดเส้นที่คั่นรูป ดีจะเป็นขีดจำกัดของการอินทิเกรตสำหรับอินทิกรัลจำกัดเขตปกติ ซึ่งเรากำลังเข้าใกล้แล้ว

การรีดิวซ์อินทิกรัลสองเท่าให้เป็นอินทิกรัลซ้ำ

กรณีพื้นที่สี่เหลี่ยม

ปล่อยให้มีอินทิกรัลสองเท่าสำหรับฟังก์ชันดังกล่าว

ถึง ประเมินอินทิกรัลสองเท่านี้ เราต้องลดมันเป็นอินทิกรัลแบบวนซ้ำซึ่งมีรูปแบบ

.

ขั้นแรก คุณต้องคำนวณอินทิกรัลจำกัดเขตด้านใน (ขวา) จากนั้นจึงคำนวณอินทิกรัลจำกัดเขตด้านนอก (ซ้าย)

คุณสามารถสลับบทบาทได้ xและ ย

.

ตัวอย่างที่ 1คำนวณอินทิกรัลสองเท่า

เราคำนวณอินทิกรัลด้านใน (ขวา) โดยถือว่า y เป็นค่าคงที่ เราเข้าใจแล้ว

.

ตัวอย่างที่ 2คำนวณอินทิกรัลสองเท่า

,

สารละลาย. เราลดอินทิกรัลสองเท่านี้เป็นอินทิกรัลแบบวนซ้ำ

ในรูปวาดเราสร้างขอบเขตการรวม:

ตอนนี้เราคำนวณอินทิกรัลด้านนอก (ซ้าย) ของอินทิกรัลภายในที่เพิ่งคำนวณ (ขวา):

ผลลัพธ์จะเป็นคำตอบของอินทิกรัลคู่นี้

คำนวณอินทิกรัลสองเท่าด้วยตัวเองแล้วดูผลเฉลย

กรณีบริเวณโค้งหรือสามเหลี่ยม

ให้เราได้รับฟังก์ชันของตัวแปรสองตัวอีกครั้ง ฉ(x, ย) และข้อจำกัดสำหรับ ดี: เป็นประเภทที่แตกต่างกันเล็กน้อยแล้ว:

รายการนี้หมายความว่าตัวเลข ดีซ้ายและขวามีจำกัด เช่นเดียวกับในกรณีของขอบเขตเป็นเส้นตรง - เส้นตรง x = กและ x = ขแต่ด้านล่างและด้านบนเป็นเส้นโค้งที่กำหนดโดยสมการ และ กล่าวอีกนัยหนึ่งและเป็นฟังก์ชัน

ให้ฟังก์ชันดังกล่าวมีอินทิกรัลสองเท่าด้วย

ในการประเมินอินทิกรัลสองเท่านี้ เราต้องลดมันเป็นอินทิกรัลแบบวนซ้ำซึ่งมีรูปแบบ

.

นี่คือข้อจำกัดของการบูรณาการ กและ ข- ตัวเลข และ - ฟังก์ชัน ในกรณีของพื้นที่สามเหลี่ยม หนึ่งในฟังก์ชันหรือเป็นสมการของเส้นตรง กรณีนี้จะกล่าวถึงในตัวอย่างที่ 3

เช่นเดียวกับในกรณีของขอบเขตเส้นตรง ขั้นแรกคุณต้องคำนวณอินทิกรัลจำกัดเขตทางขวา จากนั้นจึงคำนวณอินทิกรัลจำกัดเขตทางซ้าย

ในทำนองเดียวกัน คุณสามารถสลับบทบาทได้ xและ ย. แล้วอินทิกรัลซ้ำจะมีรูปแบบ

.

อินทิกรัลที่ซ้ำกันดังกล่าวจะต้องได้รับการแก้ไขในลักษณะเดียวกันทุกประการ: อันดับแรก - อินทิกรัลด้านใน (ขวา) จากนั้น - ด้านนอก (ซ้าย)

ตัวอย่างที่ 5คำนวณอินทิกรัลสองเท่า

,

สารละลาย. เราลดอินทิกรัลสองเท่านี้เป็นอินทิกรัลแบบวนซ้ำ

.

ในรูปวาดเราสร้างขอบเขตการรวมและเห็นว่าเป็นรูปสามเหลี่ยม:

เราคำนวณอินทิกรัลด้านใน (ขวา) โดยพิจารณาว่า x เป็นค่าคงที่ เราเข้าใจแล้ว

ตอนนี้เราคำนวณอินทิกรัลด้านนอก (ซ้าย) ของอินทิกรัลภายในที่เพิ่งคำนวณ (ขวา) อันดับแรก เราจะนำเสนออินทิกรัลนี้เป็นผลรวมของอินทิกรัล:

.

เราคำนวณเทอมแรก:

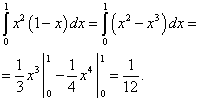
เราคำนวณเทอมที่สอง:

เราคำนวณเทอมที่สาม:

เราได้ผลรวมซึ่งจะเป็นคำตอบของอินทิกรัลคู่นี้:

.

ตัวอย่างที่ 6คำนวณอินทิกรัลสองเท่า

สารละลาย. เราลดอินทิกรัลสองเท่านี้เป็นอินทิกรัลแบบวนซ้ำ

ในรูปวาดเราสร้างขอบเขตการรวม:

เราคำนวณอินทิกรัลด้านใน (ขวา) โดยพิจารณาว่า x เป็นค่าคงที่ เราเข้าใจแล้ว

.

ตอนนี้เราคำนวณอินทิกรัลด้านนอก (ซ้าย) ของอินทิกรัลภายในที่เพิ่งคำนวณ (ขวา):

ผลลัพธ์จะเป็นคำตอบของอินทิกรัลคู่นี้

x-ถูกและผิด ย- โดเมนการรวมที่ถูกต้องและไม่ถูกต้อง

มันเกิดขึ้นที่โดเมนของอินทิกรัลของอินทิกรัลคู่ถูกจำกัดด้วยบรรทัดจนจำเป็นต้องแบ่งโดเมนของอินทิกรัลออกเป็นส่วน ๆ และแก้อินทิกรัลซ้ำแต่ละอันที่สอดคล้องกันแยกกัน เหล่านี้เป็นกรณีที่:

1) พื้นที่บูรณาการคือรูปที่มีเส้นตรงหรือเส้นโค้งตั้งแต่สองเส้นขึ้นไปในรูปแบบของขอบเขตล่างหรือบน (ซ้ายหรือขวา)

2) ขอบเขตของการบูรณาการคือตัวเลขที่มีขอบเขตของเส้นตัดกันที่มากกว่าสองจุด

หากสิ่งที่กล่าวข้างต้นใช้กับขอบเขตด้านซ้ายหรือด้านขวาของโดเมนการรวม นั่นคือ ข้อจำกัดที่กำหนดโดยบรรทัดที่แสดงในแง่ของ xจากนั้นจึงเรียกว่าโดเมนของการอินทิเกรต x-ผิด. ถ้าเป็นแนว ย = ย0 ตัดกับขอบเขตที่สอดคล้องกันที่จุดเดียวเท่านั้น และถ้าขอบเขตเป็นเพียงเส้นตรงหรือเส้นโค้งเพียงเส้นเดียว โดเมนของอินทิเกรตจะเรียกว่า x-ถูกต้อง

ในทำนองเดียวกันหากขอบเขตที่กำหนดโดยเส้นที่แสดงผ่าน ย, ตรง x = x0 ตัดกันที่มากกว่าหนึ่งจุดหรือถ้าขอบเขตเป็นเส้นตรงหรือเส้นโค้งมากกว่าหนึ่งเส้นแล้ว โดเมนของการอินทิเกรตจะเรียกว่า ย-ผิด. ตอนนี้แสดงสัญญาณ ย- พื้นที่ที่ถูกต้องน่าจะค่อนข้างง่าย

จนถึงตอนนี้เราได้ดูตัวอย่างด้วย x-ไม่ถูกต้องและ ย- พื้นที่บูรณาการที่ถูกต้อง ตอนนี้ให้พิจารณากรณีที่มีการละเมิดเงื่อนไขความถูกต้อง

ตัวอย่างที่ 7คำนวณอินทิกรัลคู่ซึ่งมีโดเมนการรวมถูกจำกัดด้วยบรรทัด ย = x , เอ็กซ์ซี = 1 , ย = 2 .

สารละลาย. ขอบเขตของการบูรณาการคือ ย-ไม่ถูกต้อง เนื่องจากไม่สามารถระบุขอบเขตด้านล่างด้วยบรรทัดเดียวได้ ย = ย(x) . ดังที่เห็นในรูปด้านบน ขอบล่างประกอบด้วย ย = x(เบอร์กันดีเข้ม) และ เอ็กซ์ซี= 1 (สีเขียว) ดังนั้นโดยตรง x= 1 (สีดำ) เราสามารถแบ่งโดเมนการรวมออกเป็นสองส่วน - และ .

อินทิกรัลคู่นี้คำนวณได้ดังนี้:

การเปลี่ยนลำดับการรวมระบบ

ตามที่กล่าวไว้ข้างต้น หลังจากที่ลดอินทิกรัลสองเท่าให้เป็นอินทิกรัลแบบวนซ้ำแล้ว คุณสามารถเปลี่ยนตัวแปรได้ xและ ยบทบาทหรืออีกนัยหนึ่งคือเปลี่ยนลำดับของการบูรณาการ

การเปลี่ยนแปลงลำดับการรวมกลุ่มสามารถอธิบายเป็นรูปเป็นร่างได้ด้วยคำพูดของ O'Henry ต่อไปนี้: "นี่คือวิธีที่ผู้อาศัยในป่า - สัตว์ - ประพฤติตัวเมื่อเขาเข้าไปในกรง และนี่คือวิธีที่ผู้อาศัยในกรง - ผู้ชาย - ประพฤติตัวเมื่อเขาหลงอยู่ในป่าแห่งความสงสัย” ตามที่ O'Henry กล่าว ผลลัพธ์ก็เหมือนกันและเหมือนกัน: “ Chalmers ฉีกจดหมายเป็นชิ้นเล็ก ๆ นับพันชิ้นและเริ่มฉีกพรมราคาแพงของเขาแล้วเดินกลับมาและ ออกมาบนนั้น” ( โอเฮนรี่. Scheherazade ของ Madison Square.)

แล้วถ้าเราอินทิกรัลซ้ายส่วนตัวแปร xและอันที่ถูกต้อง - โดย ยจากนั้นหลังจากเปลี่ยนลำดับการรวมระบบ ทุกอย่างจะกลับกัน จากนั้นขีดจำกัดของการรวมสำหรับเกม "ใหม่" จะต้อง "ยืม" จาก X "เก่า" และต้องได้รับขีดจำกัดของการรวมสำหรับ X "ใหม่" ในรูปแบบ ฟังก์ชันผกผัน, การแก้สมการ x ที่กำหนดขีดจำกัดของ y

ตัวอย่างที่ 8

.

สารละลาย. หลังจากเปลี่ยนลำดับอินทิกรัลแล้ว อินทิกรัลส่วน y จะกลายเป็นทางซ้าย และอินทิกรัลส่วน x จะกลายเป็นทางขวา เราจะยืมขีดจำกัดของการบูรณาการสำหรับเกม "ใหม่" จาก X "เก่า" นั่นคือ ขีดจำกัดล่างเท่ากับศูนย์ และขีดจำกัดบนเท่ากับหนึ่ง ขีดจำกัดของการบูรณาการสำหรับเกม "เก่า" กำหนดโดยสมการ และ หลังจากแก้สมการเหล่านี้สำหรับ x แล้ว เราก็ได้ขีดจำกัดใหม่ของการรวมสำหรับ x:

(ล่าง) และ (บน)

ดังนั้น หลังจากเปลี่ยนลำดับการอินทิเกรตแล้ว อินทิกรัลที่ซ้ำกันจะถูกเขียนดังนี้:

.

หลังจากเปลี่ยนลำดับการรวมเข้าในอินทิกรัลคู่แล้ว โดเมนของการรวมมักจะกลายเป็น ย-ไม่ถูกต้องหรือ x- ไม่ถูกต้อง (ดูย่อหน้าก่อนหน้า) จากนั้น คุณจะต้องแบ่งโดเมนการรวมออกเป็นส่วนๆ และแก้โจทย์อินทิกรัลซ้ำที่เกี่ยวข้องแต่ละรายการแยกกัน

เนื่องจากการแบ่งขอบเขตของการบูรณาการออกเป็นส่วนๆ ทำให้เกิดความยากลำบากสำหรับนักเรียนจำนวนมาก เราจะไม่จำกัดตัวเองอยู่เพียงตัวอย่างที่ให้ไว้ในย่อหน้าก่อนหน้านี้ แต่จะดูตัวอย่างเพิ่มเติมอีกสองสามตัวอย่าง

ตัวอย่างที่ 9เปลี่ยนลำดับการรวมสำหรับอินทิกรัลแบบวนซ้ำ

.

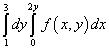สารละลาย. ดังนั้นพื้นที่อินทิกรัลของอินทิกรัลแบบวนซ้ำนี้จึงถูกจำกัดด้วยเส้นตรง ย = 1 , ย = 3 , x = 0 , x = 2ย .

เมื่อรวมเข้าด้วยกันในลำดับที่แตกต่างกัน ขอบเขตล่างของขอบเขตจะประกอบด้วยเส้นตรงสองเส้น: เอบีและ บี.ซี.ซึ่งได้จากสมการ ย= 1 และ ย = x/2 ดังรูปด้านล่าง

ทางออกของความไม่แน่นอนดังกล่าวคือการแบ่งโดเมนการบูรณาการออกเป็นสองส่วน การแบ่งโดเมนการรวมจะเป็นเส้นตรง บีเอ็ม. เราคำนวณขีดจำกัดใหม่ของอินทิเกรตโดยการค้นหาฟังก์ชันผกผัน ตามแนวทางนี้ อินทิกรัลที่ทำซ้ำหลังจากเปลี่ยนลำดับอินทิกรัลจะเท่ากับผลรวมของอินทิกรัลสองตัว:

โดยธรรมชาติแล้ว วิธีเดียวกันนี้จะเป็นคำตอบของอินทิกรัลสองเท่า ซึ่งลดเหลืออินทิกรัลซ้ำที่กำหนดในเงื่อนไขของตัวอย่างนี้

ตัวอย่างที่ 10เปลี่ยนลำดับการรวมสำหรับอินทิกรัลแบบวนซ้ำ

.

สารละลาย. ดังนั้น ขอบเขตของการอินทิเกรตของอินทิกรัลแบบวนซ้ำจึงจำกัดอยู่แค่เส้นตรง x = 0 , x= 2 และเส้นโค้ง และ .

ดังที่เห็นในรูปด้านล่างเป็นเส้นตรงที่ขนานกับแกน 0xจะตัดขอบล่างของโดเมนการรวมที่จุดมากกว่าสองจุด

ดังนั้นเราจึงแบ่งโดเมนการรวมออกเป็นสามส่วนด้วยเส้นตรง ซึ่งจะถูกวาดด้วยสีดำในรูป เราคำนวณขีดจำกัดใหม่ของอินทิเกรตโดยการค้นหาฟังก์ชันผกผัน ขีดจำกัดสำหรับสามพื้นที่ใหม่ของการรวมระบบจะเป็นดังนี้

ตามแนวทางนี้ อินทิกรัลที่ทำซ้ำหลังจากเปลี่ยนลำดับอินทิกรัลจะเท่ากับผลรวมของอินทิกรัลสามตัว:

ผลรวมที่เท่ากันของอินทิกรัลสามตัวจะเท่ากับอินทิกรัลสองเท่า ซึ่งจะลดเหลืออินทิกรัลซ้ำที่กำหนดในเงื่อนไขของตัวอย่างนี้

แต่ถึงกระนั้น เหตุสุดวิสัยมักจะรบกวนนักเรียนในขั้นตอนก่อนหน้า ซึ่งถือเป็นการกำหนดขีดจำกัดของการบูรณาการ ความวิตกกังวลและความสับสนไม่ได้เกิดขึ้นโดยไม่มีพื้นฐาน: หากจะแบ่งขอบเขตการบูรณาการออกเป็นส่วนๆ ก็มักจะเพียงพอที่จะดูภาพวาดอย่างใกล้ชิด และเพื่อแก้ปัญหาอินทิกรัลที่ทำซ้ำ - ตารางอินทิกรัล จากนั้นจำเป็นต้องมีการฝึกอบรมบางอย่างในการกำหนดขีดจำกัด ของการบูรณาการ มาดูตัวอย่างที่เราจะเน้นเฉพาะการตั้งค่าขีดจำกัดของการบูรณาการและเกือบจะอัตโนมัติในการแบ่งพาร์ติชันภูมิภาคและละเว้นโซลูชันนั้นเอง

ตัวอย่างที่ 11ค้นหาขีดจำกัดของอินทิกรัลคู่หากเป็นโดเมนของอินทิกรัล ดีให้ไว้ดังนี้:

ย - 2x ≤ 0;
2ปี - x ≥ 0;
เอ็กซ์ซี ≤ 2.

สารละลาย. อย่างชัดเจน (ผ่าน xและ ย"ไม่มีสิ่งเจือปน") ไม่ได้ระบุบรรทัดที่จำกัดขอบเขตการรวมระบบ เนื่องจากสำหรับ X ส่วนใหญ่มักจะกลายเป็นเส้นตรงที่แตะจุดหนึ่งที่ขอบเขตบนและล่างซึ่งแสดงผ่าน i จากนั้นเราจะไปตามเส้นทางนี้อย่างแน่นอน ยิ่งไปกว่านั้น เมื่อเปลี่ยนลำดับของการบูรณาการ เราจะได้ขอบเขตการรวมเข้ากับพื้นที่เดียวกัน ให้เราแก้ไขความไม่เท่าเทียมกันของเกมและรับ:

ย ≤ 2x;
ย ≥ x/2;
ย ≤ 2/x.

เราสร้างเส้นผลลัพธ์บนภาพวาด ลิมิตของอินทิเกรตส่วน x ก็คือเส้นตรงจริงๆ x= 0 และ x= 2 . แต่พื้นที่ของการบูรณาการกลายเป็น ย-ไม่ถูกต้อง เนื่องจากไม่สามารถระบุขีดจำกัดบนด้วยบรรทัดเดียวได้ ย = ย(x) .