Forelesninger: flere integraler, dobbel integraler. Multippelintegraler Definisjon av multippelintegraler

Avskrift

1 FEDERAL AGENCY FOR EDUCATION STATE EDUCATIONAL INSTITUTION OF HIGHER PROFESSIONAL EDUCATION «SAMARA STATE AEROSPACE UNIVERSITY oppkalt etter akademiker SP KOROLEVA» FLERE INTEGRALLE oppgaver og øvelser Godkjent av Redaksjonen og Publishing Board A M A metodologiske instrukser Forlag Universitetet A R A RSS

2 UDC 7 7 Utarbeidet av OM Karpilova anmelderkandidat for tekniske vitenskaper førsteamanuensis GN Gutman Flere integraler problemer og øvelser: metode for indikasjon / sammensetning OM Karpilova Samara: Samara State Aerospace University Publishing House Samlingen inneholder eksempler på løsninger på typiske problemer etter emne: doble integraler trippelintegraler anvendelser av multiple integraler I hvert tema diskuteres typiske problemer, metoder for å løse dem analyseres i detalj og problemstillinger foreslås for selvstendig arbeid Vedlegget gir muligheter for individuelle hjemmeoppgaver Alle oppgaver er satt sammen i henhold til programmet for matematikkkurset for studenter ved tekniske universiteter Metodologiske instruksjoner utarbeidet ved Institutt for generell ingeniøropplæring og beregnet på studenter ved Institutt for energi og transport ved Samara State Aerospace University UDC 7 7 Samara State Aerospace University

3 BEREGNING AV DOBBELTE INTEGRALER I KARTESISKE KOORDINATER For å beregne et dobbeltintegral, presenteres det i form av et repetert dobbeltintegral f f Løsning av eksempler Eksempel Gå fra b a f til et gjentatt integral og sett grensene for integrasjon dersom arealet begrenses av linjer: a 6; b; V; d kontur av trekant ABC hvor A; B;6C;; d Løsning: a Konstruer et område: en rett linje parallelt med O-aksen; rett linje parallelt med O-aksen; 6 linje som går gjennom punktene 6 og 6; Arealet er trekant ABC Fig. For å finne koordinatene til punktet C er det nødvendig å løse ligningssystemet Fig. 6 Derav C; Derfor, inne i regionen For å finne ut hvordan den endrer seg, tegner vi en rett linje parallelt med O-aksen og skjærer regionen. Denne rette linjen går inn i regionen langs linje a og går ut langs linje 6 eller 6. Derfor 6 Dermed er regionen kan defineres av et system av ulikheter: 6 Nå er det enkelt å sette grenser i dobbeltintegralet: f 6 f

4 b La oss konstruere: en rett parabel parallell med O-aksen Fig. Finn koordinatene til punktene A og B For å gjøre dette, løser du systemet ± Tegn en rett linje parallelt med O-aksen og skjærer området Denne linjen går inn i regionen langs en parabel og blader langs en rett linje Fig Dermed er området definert av ulikhetene f f: Derfor i La oss konstruere arealet Fig: en parabel symmetrisk om O-aksen med toppunktet i origo; den positive grenen til en parabel y symmetrisk i forhold til O-aksen med toppunktet i origo til koordinatene Fig. La oss finne skjæringspunktene til disse linjene: Ved å kvadrere begge sider av ligningen får vi Herfra. Dermed skjærer linjene ved punktene O; og A; Etter å ha tegnet en rett linje parallelt med O og kryssende området, ser vi at inngangslinjen og utgangslinjen

5 Altså: derfor f f g La oss konstruere en trekant fig Fra tegningen er det tydelig at innenfor området En rett linje parallelt med O og kryssende området går inn i trekanten langs siden AC og går ut langs siden AB Ligningen til en linje som går gjennom to punkter M og M har formen Ved hjelp av denne formelen vil vi skrive likningene til sidene AB og AC: AB: hvor er de fra; 6 AC: hvor de kommer fra Altså: Derfor f f d La oss konstruere et område For å gjøre dette transformerer vi ligningen for grensen: La oss velge et komplett kvadrat med hensyn til variabelen: Den resulterende ligningen definerer en sirkel med radius med et senter ved Et poeng; Fig Fig Fig For å sette grensene for integrasjon, må du skrive ned likningene til øvre og nedre halvdel av sirkelen til linjen for inngang til regionen og ut av regionen La oss løse den opprinnelige ligningen med hensyn til: ±

6 Det er åpenbart at øvre halvdel av sirkelen tilsvarer ligningen til den nedre Altså: derfor f f Eksempel Endre integrasjonsrekkefølgen: b 6 ; f f; a c f f Løsning: a Integrasjonsområdet er gitt av systemet med ulikheter: La oss konstruere området Fig.6: den øvre halvdelen av parablen den nedre halvdelen av parablen Ved endring av integrasjonsrekkefølgen vil integralet ha formen c f Fig. 6 La oss finne koordinatene til skjæringspunktene til parablen og den rette linjen: ± Altså A; I; La oss tegne en rett linje parallelt med O-aksen som skjærer området. Inngangslinjen til denne inn i området er en parabel, utgangslinjen er rett. Dermed kan området også defineres av et system av ulikheter: Da f f 6

7 b I dette tilfellet er integrasjonsområdet gitt av et system av ulikheter: 6 La oss konstruere dette området i Fig.7: 6 hyperbel rett linje La oss finne koordinatene til punktene A og B Ved punkt A derfor Ved punkt B derfor Dermed EN; I; Ved endring av integrasjonsrekkefølgen vil integralet ha formen f Fig. 7 c Siden da c ; La oss tegne en rett linje parallelt med O-aksen og som skjærer området. Inngangslinje 6 er en hyperbel hvorfra. Utgangslinje er en rett linje fra hvor 6 Arealet er definert av ulikhetene: 6 Vi får til slutt 6 6 f f i La oss konstruere områdene: og: Områdets grense bestemmes av ligningen ± Ved å kvadrere begge sider av ligningen får vi ligningen til parabelens toppunkt koto - svermen befinner seg i et punkt; og symmetriaksen er O-aksen Fig. Områdets grense er gitt ved følgende ligninger: en rett linje som går gjennom origo for koordinater og den øvre grenen av parabelen.. Dermed er integrasjonsområdet Fig. 7

8 For å sette grensene for integrasjon vil vi finne koordinatene til skjæringspunktene til grenselinjene For å gjøre dette skal vi løse ligningssystemet; Derfor dermed A; I; Ved endring av integrasjonsrekkefølgen vil vi ta det ytre integralet over variabelen, det indre. Derfor tegner vi en rett linje som skjærer området og parallelt med Ox-aksen. Den kommer inn i området langs en linje og går ut langs linjen Så, ved å endre rekkefølgen på integrasjonen, får vi f f f Her, endring av integrasjonsrekkefølgen forenkler beregningene, siden du i stedet for å beregne to integraler trenger å beregne bare ett Eksempel Beregn; ; hvor arealet er begrenset av linjer Løsning La oss konstruere arealet Fig. 9: en rett linje parallelt med O-aksen og rette linjer som går gjennom origo for koordinater For å beregne integralet, la oss gå fra dobbeltintegralet til det gjentatte. Siden arealet kan defineres av et system av ulikheter: så beregner vi først det interne integralet, og betrakter det som en konstant verdi siden integrasjon utføres over variabelen: Nå gjenstår det å beregne det resulterende eksterne integralet:

9 Således Eksempel Beregn Løsning Konstruer et område: O-aksen er en rett linje parallelt med O-aksen, en rett linje som går gjennom origo til koordinater Fig. Rette linjer og skjærer i punkt A; Går vi til dobbeltintegralet og beregner det, får vi om det er begrenset av linjer i henhold til reduksjonsformlene Fig. 9

10 Problemer for uavhengig løsning Ordne grensene for integrasjon i gjentatte integraler som f reduseres til hvis arealet begrenses av linjene: a; b; V; G; d trekant ABC hvor A; I; MED; Endre rekkefølgen for integrering: a f ; b f; i f; g f Beregn doble integraler forutsatt at arealet er begrenset av de angitte linjene: a; 7; b; ; V; ; g e; 6 svar a f ; b f; i g f; d a f; b f f ; i f; g f a; 7b; V; f 6 g e f ;

11 DOBBELT INTEGRAL I POLARKOORDINATER Hvis både kartesiske og polare koordinatsystemer er gitt på planet og polen sammenfaller med origo for koordinater og polaraksen er på linje med Ox-aksen, så for å gå til polare koordinater, bruk formlene Fig. Dessuten, hvis området er begrenset av stråler α β og kurver Fig. f β α f Løsning av eksempler Eksempel Beregn > Løsning La oss konstruere et område på Fig: en sirkel med radius, rette linjer som går gjennom origo for koordinater Siden området er en del av en sirkel, er det praktisk å gå til polare koordinater. I dette tilfellet er polen kompatibel med punkt O; og la polaraksen ligge langs O-aksen Så der arealet er begrenset av linjer Fig Nå må vi beskrive arealet i det polare koordinatsystemet Vinkelen inne i området varierer fra til cm Fig Rett k er skråstilt mot O-aksen

12 i en vinkel hvis tangent er lik k Derfor tg ; tg Herfra; Så, inne i regionen, forlater en stråle som kommer fra polen O og krysser området langs en sirkel, hvis likning i polare koordinater har formen. Dermed er regionen beskrevet av et system av ulikheter: Nå er det lett å plassere grenser i det gjentatte integralet og regn det ut Eksempel Regn ut e hvor ringen Løsning Siden området er begrenset av sirkler 9 og 9 Fig. er det praktisk å bytte til polare koordinater: Da vil grenselikningene ta formen; 9 Fig. For å sette grensene for integrasjon i det gjentatte integralet, legger vi merke til at innenfor området tar vinkelen alle verdier fra til La oss tegne en stråle fra opprinnelsen til koordinatene som skjærer området. Den går inn i regionen langs en linje og blader langs linjen Dermed: Så

13 9 9 9 eee eee eee eee Eksempel Regn ut om er bestemt av ulikheter: Løsning La oss konstruere et område For å gjøre dette transformerer vi ligningen til grensen: Så grensen er en sirkel med radius med et senter i et punkt; Siden da er den øvre halvdelen av sirkelen Fig La oss gå videre til polare koordinater: Fig Grenseligningen i polare koordinater vil ha formen Forutsatt at vi får Området er helt lokalisert i første kvartal, derfor i polare koordinater er arealet gitt ved ulikhetene Nå kan vi beregne dobbeltintegralet

14 Oppgaver for uavhengig løsning Regn ut ved å flytte til polare koordinater: der øvre halvdel av sirkelen 6 hvor arealet tilfredsstiller ulikhetene der arealet er begrenset av linjene 9 6 der begrenses av linjene 6 der arealet er begrenset av kurver Svar; ; ; ; ANVENDELSE AV DOBBELTE INTEGRALER Dobbeltintegralet brukes til å beregne: og arealet til en plan figur begrenset av området: S; b volumet til et sylindrisk legeme begrenset ovenfra av en kontinuerlig overflate f nedenfra av et plan og fra siden av en rett sylindrisk overflate som skjærer ut et område på planet O:

15f; i overflatearealet gitt av ligningen f, hvis projeksjon på planet O er regionen: σ I tillegg brukes doble integraler i mekanikk for å beregne: og massen til en flat plate som opptar området til planet O og som har en variabel overflatetetthet y y: M y; b statistiske momenter av platen i forhold til O- og O-aksene: ; M y; M γ i koordinatene til tyngdepunktet til platen: γ M c; M γ Løsning av eksempler ц M M γ γ 6 Eksempel Finn arealet av området avgrenset av linjene Løsning La oss konstruere regionen Likningen definerer en parabel, likningen til en rett linje som går gjennom origo til koordinatene Fig. For å finne skjæringspunktene til disse linjene, løser vi ligningssystemet: Herfra Så. Dermed skjærer den rette linjen parabelen i punkter; og A; Bruk formelen S Fig Eksempel Finn arealet til en figur avgrenset av linjer utenfor den første sirkelen;

16 Løsning Ligningen spesifiserer en sirkel med radius med et sentrum ved origo av koordinater Ligningen spesifiserer en sirkel med radius med et sentrum i punktet La oss løse ligningssystemet sammen ± Altså; EN; B AmBn-regionen kan spesifiseres ved ulikheter ved å bruke formel 6 S Eksempel Finn volumet til et legeme avgrenset av koordinatplan og et plan Løsning La oss konstruere kroppen Fig. 7 og dens projeksjon på planet O Fig. 6

17 I henhold til formelen Fig. 7 Fig. I eksemplet er arealet trekanten OAB vist i Fig. og overflaten bestemmes av likningen til planet hvorfra Således Eksempel Finn volumet til et legeme begrenset av koordinatplanene av planet og overflaten Løsning Kroppen er vist i Fig. 9 Planet går parallelt med O-aksen; en paraboloid hvis toppunkt er på punktet;; Projeksjonen av legemet på planet O er trekanten ABO fig AB skjæringslinjen mellom planet og planet derfor ligningen for den rette linjen AB: derfra 7

18 Bruke formelen Fig. 9 Fig. med en sylinder 6 Eksempel Finn volumet til et legeme avgrenset av en paraboloid og plan og Løsning Kroppen er vist i Fig. For enkelhets skyld ved å sette grensene for integrasjon, konstruerer vi projeksjonen av kroppen på planet O Fig. Ved å bruke formelen Fig. Fig.

19 7 6 Eksempel 6 Finn volumet til et legeme avgrenset av flater 7 Løsning Denne kroppen er avgrenset av to paraboloider Fig. Skjæringslinjen til paraboloider bestemmes av et ligningssystem Fra den første ligningen Så skjæringslinjen er en sirkel av radius som ligger i planet: Projeksjonen av denne linjen på planet O er også en sirkel, så det er praktisk å gå til de polare koordinatene Fig. Volumet til et legeme kan beregnes som forskjellen mellom volumene til to sylindriske kropper: Eksempel 7 Finn overflatearealet til en kule inne i en sylinder 9 Løsning En sylinder skjærer ut to deler på overflaten av kulen som er symmetriske i forhold til planet O Fig. På grunn av symmetri er det nok å beregne overflatearealet av bare den øvre "hetten" og doble resultatet 9

20 For å regne bruker vi formelen Siden den inkluderer partielle deriverte, regner vi og Vi har derfor fra likningen til en kule Da Fig Altså, ifølge formelen σ Projeksjon av overflaten på planet O-sirkel, er det praktisk å gå til polare koordinater I det polare koordinatsystemet ser likningen til en sirkel slik ut Så i polare koordinater σ 9 vil derfor 9 akseptere Siden vi betraktet arealet til bare den øvre "hetten", så er hele overflatearealet lik σ σ n Eksempel Finn tyngdepunktet til en homogen plate ABC hvis A;- B; C; ;- Løsning For å beregne koordinatene til tyngdepunktet skal vi bruke formlene 6 Siden platen er homogen er overflatetettheten γ konstant, derfor vil formlene ha formen q; ts

21 Fra figuren i Fig. er det tydelig at platen har form som en trapes og er symmetrisk i forhold til O-aksen, derfor La oss skrive ned likningene til rette linjer BC og A ved å bruke formelen som bestemmer likningen til en rett linje som går gjennom to gitte punkter: c BC: ; A: Fig La oss nå separat beregne telleren og nevneren til brøken som bestemmer koordinaten: q 9 Nevneren inneholder et integral som er lik arealet av regionen og arealet til trapeset ABC Derfor h ; du kan beregne dette AB C-integralet direkte, altså c; q Eksempel 9 Finn massen til den øvre halvdelen av ellipsen hvis tettheten i hvert punkt er lik ordinaten til punkt b a Løsning Tettheten i hvert punkt er lik ordinaten γ I følge formelen M γ For den øvre halvdelen av ellipsen, Fig. 6 b derfor a Fig. 6

22 M a a a a b a b a a b a a b a a a a b Problemer for uavhengig løsning a ab Finn arealet av figuren avgrenset av linjene: a; b; i en ; g a a; d Finn volumet av legemet avgrenset av overflatene: a; b; i en; d Finn arealet av den indikerte overflaten: a av delen av planet 6 som er innelukket i den første oktanten; b del av plan a utskjært av sylinder a; i en paraboloid inne i en sylinder; g av en paraboloid avskåret av en parabolsylinder og et plan Finn tyngdepunktet til trapeset ABC hvor A; B; C; ; hvis tettheten i hvert punkt er lik abscissen til dette punktet Finn tyngdepunktet til en homogen figur avgrenset av en parabel og en rett linje 6 Finn massen til en sirkulær plate med radius hvis overflatetettheten i hvert punkt er proporsjonal til avstanden fra sentrum av sirkelen Svar a; b; V; g a a; d 6 a 6; b; i en ; g a a

23a; b a; V; g c c c c 6 6 k BEREGNING AV TRIPLE INTEGRALER I KARTESISKE KOORDINATER For å beregne et trippelintegral, er det representert som et trippelintegral: Løsning av eksempler Eksempel Gå fra f b a f f til trippel og sett grensene for integrasjon dersom arealet er begrenset av: et plan og koordinere fly; b kjegle og plan h; i en ball Løsning a La oss konstruere et område og projeksjonen av dette området på planet O Fig. 7 Rett AB er skjæringslinjen mellom planet og planet, derfor ligningen dens Dermed er dette OAB Fig. 7 Fig Fra Fig. det er lett å se at Ved å tegne en rett linje parallelt med O-aksen og skjære trekanten OAB Fig., legger vi merke til at hun går inn langs linjen og går langs linjen

24 For å finne ut grensene for endring trekker vi en rett linje parallelt med O-aksen og skjærer området Fig. 7 Den kommer inn i området langs overflaten og går ut langs overflaten.Dermed kan området beskrives ved et system av ulikheter 6 derfor f f 6 b For å sette grensene i trippelintegralet konstruerer vi arealet og dets projeksjon på plan O-region Fig. 9 Ligningen til linjen som avgrenser området fås ved å løse ligningssystemet h h Fig. 9 At er, en sirkel med radius h med sentrum i origo for koordinatene Tegn rette linjer parallelle med O og O som krysser hverandre og vi får det som beskrives av ulikhetssystemet h h h h h Derfor h h h h f f

25 Du kan velge en annen integrasjonsrekkefølge i et trippelintegral, da vil naturlig nok også grensene for integrasjon endres La oss for eksempel forestille oss det opprinnelige integralet i formen c f For å sette grensene for integrasjon, projiserer vi på planet O og tegne rette linjer parallelt med O og O og kryssende henholdsvis og Fig. I dette tilfellet er det gitt av ulikhetene: h derfor h f f Fig c La oss konstruere området og dets projeksjon på planet O Fig Fig Fra tegningen er det klart det

26 f f f f Eksempel Regn ut om et legeme er begrenset av koordinatplanene til et plan og en kjegle Løsning La oss konstruere et legeme og dets projeksjon på planet O Fig. Fra tegningen er det tydelig at det er beskrevet av ulikhetene: Fig Således 6 6

27 Problemer for uavhengig løsning Gå fra f til en trippel integral og sett grensene for integrasjon dersom kroppen er begrenset: a av en ellipsoide; 9 b paraboloid og plan; i koordinatplan og et plan 6 Regn ut om kroppen er begrenset av plan og en kule. b f; in f 6 ENDRING AV VARIABLER I DE TRIPLE INTEGRAL SYLINDRISKE OG SFERISKE KOORDINATER Formler for overgang til sylindriske koordinater Fig: ; ; ; Formler for overgang til sfæriske koordinater θ r Fig: r θ ; r θ; r θ; r θrθ Her; θ ; r 7

28 Løsning av eksempler Eksempel Beregn Fig Fig hvis begrenset av en kjegle og et plan Løsning Kroppen er avbildet i Fig. Skjæringslinjen mellom kjeglen og planet har ligningen te. Dermed er projeksjonen av kroppen på planet O-sirkelen Fig6 Fig Fig 6 La oss gå videre til sylindriske koordinater: ; ; ; I disse koordinatene er likningen av sirkelen vist i fig. 6, likningen av kjeglen og kroppen gitt av ulikhetene; ; Så

29 v Eksempel Regn ut om kroppen er begrenset av overflater Løsning Konstruer en region; plan For å konstruere en flate, transformerer vi ligningen: Denne ligningen definerer en sirkulær sylinder ved bunnen av denne ligger en sirkel med radius med et sentrum i punktet;; Dermed er integrasjonsområdet en sylinder, Fig. 7. Derfor er det praktisk å bruke sylindriske koordinater I disse koordinatene vil ligningen til den sylindriske overflaten som avgrenser integrasjonsområdet ha formen Det vil si hvorfra Basert på dette, regionen kan beskrives ved et system av ulikheter; ; Fig 7 9

30 Så Eksempel Regn ut hvor kroppen er den øvre halvdelen av ballen Løsning Siden integrasjonsområdet her er en del av ballen, er det praktisk å gå til sfæriske koordinater: r r r r r r r r r r r r r r r θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ Problemer for uavhengig løsning Beregn om begrensede overflater Beregn hvor avgrenset av overflater

31 Beregn Beregn om begrenset til overflater hvis en ball Svar ANVENDELSE AV TRIPLE INTEGRALER Trippelintegralet brukes ved beregning av: og volumet av en kropp Ω: ; 7 Ω b kroppsmasse som opptar et område Ω med variabel volumetrisk tetthet γ: M γ ; Ω i koordinatene til kroppens tyngdepunkt Ω: q γ M Ω q γ 9 M Ω q γ M Ω der M er massen til kroppen. Hvis kroppen er homogen, kan vi i formlene 9 sette γ ; M Løsning av eksempler Eksempel Finn volumet til et legeme avgrenset av en sylinder og plan Løsning Legemet og dets projeksjon på planet O er vist i Fig. Fig. For å finne koordinatene til punktene A og B, løser vi ligningssystemet :

32±A; B; Dermed er regionen Ω beskrevet av et system av ulikheter; ; Bruk formelen 7 Ω Eksempel Finn massen til et legeme avgrenset av plan hvis tettheten i hvert punkt er γ Løsning La oss konstruere et legeme Ω og dets projeksjon på planet O Fig. 9 Fig. 9 Planet skjærer planet langs en rettlinje linje Ved å løse systemet får vi koordinatene til punkt A; Dermed er kroppen Ω beskrevet av et system av ulikheter; ; Ved å bruke formelen kroppsmasse M Ω Eksempel Beregn massen til et legeme avgrenset av plan 9 og en parabolsylinder hvis tettheten i hvert punkt er proporsjonal med abscissen og i en enhetsavstand fra planet O er lik

33 Løsningstetthet er proporsjonal med abscissen; derfor k γ Ved enhetsavstand fra O-planet er tettheten lik; derfor for γ Da k k Dermed γ Konstruer legemet Ω og dets projeksjon på planet O Fig Fig For å finne koordinatene til punkt A, løs ligningssystemet; 9 A Dermed kan arealet defineres av ulikhetssystemet Ω Ω 9: I følge formelen er kroppens masse lik Ω M Eksempel Finn koordinatene til tyngdepunktet til et legeme avgrenset av nedre halvdel av sfæren og en paraboloid hvis tettheten i hvert punkt er proporsjonal med kvadratet på avstanden fra O-aksen

34 Løsning La oss konstruere en kropp Toppen av paraboloiden er et punkt; ; Ligningen er i kan transformeres til den formen at den definerer en kule med radius med et senter i et punkt; ; Så kroppen har formen vist i fig. Projeksjonen av denne kroppen på planet O er en sirkel. Ligningen kan fås ved å løse ligningssystemet. I planet har ligningen til skjæringslinjen formen. ligning av projeksjonen av kroppen Ω på planet har samme form Ω Fig. Siden sirkelen er praktisk ved beregning, gå til sylindriske koordinater ; ; I disse koordinatene har ligningen for grensen Ω formen; og vinkelen tilfredsstiller betingelsen Ligning av en paraboloid i sylindriske koordinater hvorfra Ligning av en kule: ± For den nedre halvdel Variabel tetthet i henhold til betingelsene for problemet er proporsjonal med kvadratet av avstanden fra O-aksen som γ k In sylindriske koordinater γ k Siden kroppen er symmetrisk om O-aksen, er det åpenbart at tyngdepunktet ligger på denne aksen er q; q For å beregne q bruker vi formel 9: q γ M Ω La oss først beregne massen til kroppen M [formel ]:

35 6 k k k k k k k k M γ Ω Ω Ω La oss nå beregne Ω Ω Ω γ k k k k k k k k k k k Ifølge formelen k k c Så tyngdepunktet til den aktuelle kroppen har koordinater; ; 7

36 Oppgaver for uavhengig løsning 6 Finn volumet til en kropp avgrenset av: et plan; b paraboloid og plan; i flater og 6 Finn massen til et legeme begrenset: a av kuler hvis tettheten er γ k ; b overflater hvis tettheten er γ k ; i en kjegle og et plan b hvis tettheten er proporsjonal med ordinaten til punktet og i en enhetsavstand fra planet O er lik γ 6 Finn koordinatene til tyngdepunktet til et homogent legeme avgrenset av plan a Svar 6a; b; i 6 9 k γb 6 a k ; b; ved 66C; 6

37 Alternativ VEDLEGG ALTERNATIVER FOR INDIVIDUELLE LEKSER Finn tyngdepunktet til en flat figur avgrenset av linjer Finn overflatearealet til en sylinder innelukket inne i sylinderen Finn volumet til en kropp avgrenset av overflater Finn massen til en kropp avgrenset av en kule og en paraboloid hvis tettheten på et hvilket som helst punkt er lik applikatet til dette punktet Alternativ Finn tyngdepunktet til en flat figur avgrenset av en linje og en halvbølgesinusformet Finn overflatearealet til en kjegle avskåret av fly Finn volumet til et legeme avgrenset av overflater Finn massen til et legeme avgrenset av en del av en kule med radius i den første oktanten hvis tettheten på et hvilket som helst punkt er lik avstanden fra punktet til planet O Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer Finn overflatearealet til en kjegle inne i sylinderen 9 Finn volumet til et legeme avgrenset av overflater 9 9 Finn massen til et legeme avgrenset av et sfærisk lag mellom flater 9 og 6 hvis tettheten i hvert punkt er omvendt proporsjonal med avstanden fra punktet til origo for koordinatene Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer 6 > Finn overflatearealet inne i sylinderen 6 Finn volumet til en kropp avgrenset av overflater 7

38 Finn massen til et legeme avgrenset av en rett sirkulær sylinder med radius i høyden hvis tettheten i hvert punkt er lik kvadratet på avstanden fra punktet til symmetriaksen til sylinderen Alternativ Finn tyngdepunktet til en flat figur avgrenset av en sirkel sentrert ved opprinnelsen til koordinatene med en radius og to stråler plassert symmetrisk i forhold til O-aksen og danner hverandres vinkel Finn overflatearealet til en kjegle som ligger inne i sylinderen Finn volumet til et legeme avgrenset ved overflater Finn massen til et legeme avgrenset av koordinatplan og plan 6 hvis tettheten i hvert punkt er lik abscissen til dette punktet Alternativ 6 Finn tyngdepunktet til en flat figur avgrenset av O-aksen og den øvre delen av ellipsen b a Finn overflatearealet til sylinderen avskåret av fly Finn volumet til et legeme avgrenset av overflater 6 Finn massen til et legeme avgrenset av overflater 6 hvis tettheten i hvert punkt er lik applikatet til dette punktet Alternativ 7 Finn tyngdepunktet til en flat figur avgrenset av en kardioide 7 Finn overflatearealet til en kjegle skåret ut av en sylinder Instruksjoner Gå til polare koordinater Finn volumet til en kropp avgrenset av overflater Finn massen til en kropp avgrenset ved flater > hvis tettheten er lik ordinaten til punktet Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer p

39 Finn overflatearealet til en paraboloid inne i en sylinder Finn volumet til et legeme avgrenset av overflater 6 Finn massen til et legeme avgrenset av overflater hvis tettheten i hvert punkt er lik Alternativ 9 Finn tyngdepunktet til en flat figur avgrenset av linjer 9 9 > Finn overflatearealet til et legeme avgrenset av en kule og en paraboloid Finn volumet til et legeme avgrenset av overflater 6 9 utenfor sylinderen Finn massen til et legeme avgrenset av et sfærisk lag mellom flater 6 hvis tettheten er omvendt proporsjonal med avstanden til punktet fra origo for koordinater Alternativ Finn tyngdepunktet til en flat figur avgrenset av en linje og rett linje OA som går gjennom origo for koordinater og punkt A; Finn overflatearealet til en kule skåret ut av en sylinder Finn volumet til et legeme avgrenset av overflater; inne i sylindre Finn massen til et legeme avgrenset av en kule med en radius hvis tettheten er proporsjonal med kuben av avstanden fra midten av ballen og ved en enhetsavstand er lik γ; Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer 6 Finn overflatearealet til en sylinder mellom planene Finn volumet til et legeme avgrenset av overflater Finn massen til et legeme avgrenset av en sylindrisk overflate og plan hvis tettheten er lik ordinaten til punktet 9

40 Alternativ Finn tyngdepunktet til en flat figur avgrenset av en kardioide Finn overflatearealet til en ball innelukket i en sylinder Finn volumet til en kropp avgrenset av overflater Finn massen til en kropp avgrenset av en oktant av en ball ved koordinatplan og et plan hvis tettheten i hvert punkt er lik applikatet til dette punktet Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer Finn arealet til en paraboloid innelukket mellom en sylinder og et plan c a b Finn masse av et legeme avgrenset av en paraboloid og et plan hvis tettheten er lik summen av kvadratene til koordinatene til punktet Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer Finn overflatearealet til en sylinder innelukket mellom planet O og overflaten Finn volumet til et legeme avgrenset av overflater Finn massen til et legeme avgrenset av en sylinder 6 hvis tettheten er proporsjonal med kvadratet på avstanden fra punktet til sylinderens akse Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer α α tg tg Finn overflatearealet til en kjegle plassert inne i sylinderen Finn volumet til et legeme avgrenset av overflater

41 Finn massen til et legeme avgrenset av overflater > hvis tettheten er lik ordinaten til punktet Alternativ 6 Finn tyngdepunktet til en flat figur avgrenset av linjer 6 Finn overflaten til en kule 6 inne i sylindrene Finn volumet til et legeme avgrenset av flater b a a b Finn massen til et legeme avgrenset av flater hvis tettheten er lik applikatet til punktet Alternativ 7 Finn tyngdepunktet til en likebenet rettvinklet trekant med et ben hvis tettheten ved hver punktet er proporsjonalt med kvadratet av avstanden fra toppunktet til den rette vinkelen Finn overflatearealet til kjeglen skåret ut av sylinderen Instruksjoner Gå til polare koordinater Finn volumet til et legeme avgrenset av overflater 9 Finn massen til en kule med radius hvis tettheten er proporsjonal med kuben av avstanden fra midten av ballen og per enhet avstand lik γ Option Finn tyngdepunktet til en flat figur avgrenset av linjer Finn overflaten til en paraboloid innelukket i den første oktanten En paraboloid er avgrenset av et plan 6 Finn volumet til et legeme avgrenset av overflater 6 Finn massen til en del av en kule med radius i den første oktanten hvis tettheten i hvert punkt er lik avstand fra planet O Alternativ 9 Finn tyngdepunktet til en flat figur avgrenset av linjer Finn overflatearealet til et legeme avgrenset av en kule og en paraboloid

42 Finn volumet til et legeme avgrenset av overflater Finn massen til et legeme avgrenset av en rett sirkulær sylinder med en høyderadius hvis tettheten er lik kvadratet på avstanden til punktet fra midten av sylinderbunnen Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer > Finn overflatearealet til en kule 9 skåret ut av en sylinder Finn volumet til et legeme avgrenset av overflater Finn massen til en kule med radius hvis tettheten er proporsjonal med kuben av avstanden fra sentrum og ved en enhetsavstand er lik γ Option Finn tyngdepunktet til en flat figur avgrenset av linjer ± tg 6 Finn overflatearealet til en sylinder inne i en sylinder Finn volumet til et legeme avgrenset av overflater inne i en sylinder Finn massen til et legeme avgrenset av fellesdelen av to kuler hvis tettheten er proporsjonal med avstanden fra punkter til plan O Alternativ Finn tyngdepunktet til en flat figur avgrenset av en kardioide Finn overflatearealet til en kjegle avskåret av fly Finn volumet til et legeme avgrenset av overflater utenfor sylinderen 6 Finn massen til en del av en kule med radius i den første oktanten hvis tettheten i hvert punkt er lik avstanden til planet O

43 Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer Finn overflatearealet til en paraboloid 6 innelukket mellom en sylinder og et plan Finn volumet til et legeme avgrenset av overflater Finn massen til et legeme avgrenset av en sfærisk lag mellom flater 6 hvis tettheten er omvendt proporsjonal med avstanden fra origo Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer 9 Finn overflatearealet som ligger inne i sylinderen Finn volumet til et legeme avgrenset av overflater Finn massen av et legeme avgrenset av en paraboloid og et plan hvis tettheten er lik summen av kvadratene til koordinatene til punktet Alternativ Finn tyngdepunktet til en flat figur avgrenset av linjer Finn overflatearealet til en kjegle inni en sylinder Finn volumet til et legeme avgrenset av overflater Finn massen til et legeme avgrenset av en felles del to kuler hvis tettheten er proporsjonal med avstanden fra punktet til planet O

44 INNHOLD BEREGNING AV DOBBELTE INTEGRALER I KARTESISKE KOORDINATER DOBBELT INTEGRALER I POLARKOORDINATER APPLIKASJONER AV DOBBELTE INTEGRALER BEREGNING AV TRIPLE INTEGRALER I KARTESISKE KOORDINATER ERSTATNING AV VARIABLER INTEGRALER I TRIPLE 7 ANVENDELSE AV TRIPLE INTEGRALER VEDLEGG ALTERNATIVER FOR INDIVIDUELLE LEKSER 7 Pedagogisk utgave FLERE INTEGRALS problemer og øvelser Metodologiske instruksjoner Satt sammen av Olga Mikhailovna Karpilova Redaktør Yu N Litvinova Samling Yu N Litvinova Signert for trykk Format 6x/6 Offsetpapir Offsettrykk Tilstand l 7 Kopiopplag Bestill Kunst S- 9/ Samara State Aerospace University 6 Samara Moskovskoe Highway Publishing House of Samara State Aerospace University 6 Samara Moskovskoe Highway

Cos, sin, J dd dd d d 5 Regn ut zdd zddz ddz, hvor yttersiden av overflaten z, avskåret av planet z Løsning Flaten er en paraboloid definert eksplisitt av ligningen z Derfor

STATLIG INSTITUTION FOR HØYERE PROFESJONELL UTDANNING "HVITERUSSISK-RUSSISK UNIVERSITET" Institutt for "Høyre matematikk" HØYERE MATEMATIKK. MATEMATIKK. MATEMATIKK (SPESIELLE KAPITLER). MATEMATISK ANALYSE

METODOLOGISKE INSTRUKSJONER FOR BEREGNINGSOPPGAVE I LØPET AV HØYERE MATEMATIKK «ORDINÆRE DIFFERENSIALLIGNINGER SERIEN MULTIPLE INTEGRALER» DEL III TEMA FLERE INTEGRALER INNHOLD Beregning av dobbel og trippel

Transportdepartementet i den russiske føderasjonen Federal State Budgetary Educational Institution of Higher Education "Russian University of Transport (MIIT)" ITTSU Department of "Higher and Computing"

Utdannings- og vitenskapsdepartementet i den russiske føderasjonen Federal State Budgetary Education Institute of Higher Professional Education "Siberian State Industrial University"

PRAKTISK LEKSJON 9 Beregning av dobbeltintegral i polare koordinater Anvendelser av doble integraler La oss se på et spesielt tilfelle av endring av variabler som ofte brukes ved beregning av dobbeltintegraler

Doble integraler Eksempler på å løse problemer 1. Reduser dobbelintegralet f(x, y) dx dy til den gjentatte på to måter (ved formel (1) og ved formel (2)), hvis G er et område avgrenset av kurvene x = 1, y = x 2, y =

Uttrykk av kroppsmasse gjennom et trippelintegral i sylindriske koordinater Definisjoner og formler for å løse problemer Definisjon En sylindrisk stråle orientert langs O-aksen Fig. Et begrenset legeme G kalles

Utdanningsdepartementet i Republikken Hviterussland HVITERUSSISK NATIONAL TECHNICAL UNIVERSITY Institutt for ingeniørmatematikk N.A. Kondratyeva O.G. Vishnevskaya N.K. Prikhach MATEMATIKK Metodologisk manual

Manualen er beregnet på deltidsstudenter ved KSTU i andre studieår. Håndboken dekker følgende emner i en kortfattet og tilgjengelig form: Multiple integraler, Kurvilineære integraler, Serier, Sannsynlighetsteori.

Vitenskaps- og utdanningsdepartementet i den russiske føderasjonen Moskva statsuniversitet for geodesi og kartografi AV Aristarkhova, NG Babaeva Individuelle oppgaver i høyere matematikk FLERE INTEGRALER

PROBLEMBANK OM EMNET "INTEGRAL BEREGNING" * Endre rekkefølgen for integrering + d d * Finn arealet av et flatt område avgrenset av linjene =, =, = * Beregn (D) + acctg d, hvor) +, + 9, = (D-område,

KULTURDEPARTEMENTET I DEN RUSSISKE FEDERASJONEN FORBUNDSSTATSBUDSJETT UTDANNINGSINSTITUSJONEN FOR HØYERE PROFESJONELL UDDANNELSE ST. PETERSBURG STATSUNSITET FOR KINO OG

Del. Eksempel på eksamensoppgaver i matematikk A. De enkleste oppgavene for tre poeng.. Beregn arcsin-integraler e) II semester av ISiA, og 9 gr. i) 6 n j) 5 6 5 g) 6 d) cos h) z arcsin z. Beregn deriverte

TRANSPORTDEPARTEMENTET FOR DEN RUSSISKE FØDERASJONEN FEDERAL STATE BUDGETARY EDUCATIONAL EDUCATIONAL EDUCATION INSTITUTION OF HIGH EDUCATION "RUSSIAN UNIVERSITY OF TRANSPORT (MIIT)" Institute of Transport Technology

Region 3 (D) I vårt tilfelle er n normalvektoren til XOY-planet, de n k ( ) = ϕ, ϕ, deretter = =, og n ( ) cos γ =, + + (ϕ) (ϕ) (ϕ) (ϕ) dq = + + dd Merk Hvis overflaten (Q) er riktig i retningen

MATEMATIKKOPPGAVE (tekniske fakulteter, semester) 7 Integraler Finn integralene d d sin + d + + d + d + d 7 (+) d + + 8 d 9 cos d cos + d cos d + 8 d 9 d d + d 9 + d + 7 tg d 8 cosd cos sin 9 d

FOREDRAG N 45 Multippelintegraler i polare, sylindriske og sfæriske koordinater Anvendelser av multiple integraler Dobbeltintegral i polare koordinater Trippelintegral i sylindriske og sfæriske koordinater

Kapittel. Flere integraler.. Leksjon... Redusere en dobbel integral til en gjentatt. Ved beregning av doble integraler, bør to tilfeller skilles. () Første tilfelle. Integrasjonsregionen er begrenset til venstre

HØYERE KOMMUNIKASJONSSAMLING AV STANDARDBEREGNINGER i faget "HØYERE MATEMATIKK" del II for studenter av spesialiteten T 000 Posttjenester Minsk 00 Satt sammen av Ryabenkova LA Publikasjonen ble godkjent på møtet

FORelesning Andreordens linjer hyperbel Som eksempel vil vi finne ligninger som definerer en sirkel, parabel, ellipse og sirkel En sirkel er et sett med punkter på et plan like langt fra en gitt.

Trippel integral Volchenko Yu.M. Forelesningsinnhold Konseptet med en trippelintegral. Betingelsene for dens eksistens. Middelverditeorem. Beregning av trippelintegralet i kartesiske og krumlinjede koordinater. Trippel

FOREDRAG N. Beregning av multiple integraler..beregning av et dobbeltintegral i rektangulære kartesiske koordinater.....beregning av et dobbeltintegral (vilkårlig område)...trippelintegral.....beregning

Introduksjon Retningslinjene inneholder 26 versjoner av individuelle lekser om temaene «Rett linje på et plan og i rommet», «Fly», «Kurver og andreordens flater». Under individuelle

Innhold Introduksjon Multiple, krumlinjede og overflateintegraler Elementer i feltteori Oppgaver til klasseromstimer Kort informasjon fra teorien Eksempler på problemløsning Oppgaver for selvforberedelse Test

Praktisk leksjon 6 Overflateintegraler 6 Definisjon av egenskapen, beregning og anvendelser av overflateintegralen av th type 6 Definisjon av egenskapen og beregning av overflateintegralen av th type 6 Definisjon

B. M. Mavrin, E. I. Balaev IMAGE OF BODIES OF ROTATION Workshop Samara 2005 FEDERAL AGENCY FOR EDUCATION STATLIG UTDANNINGSINSTITUT FOR HØYERE PROFESJONELL UTDANNELSE “SAMARSKY”

Doble integraler Oppgaver og øvelser for selvstendig arbeid 1. Reduser dobbelintegralet f(x, y) dx dy til et gjentatt integral på to måter hvis: G a) G er en trekant med toppunkter (1, 1), (4, 1) ), (4, 4); b)

Federal Agency for Railway Transport Ural State Transport University Institutt for høyere matematikk I N Pirogova Analytisk geometri i eksempler og problemer Jekaterinburg

Leksjon 1-2. Bestemt integral og dets anvendelser I. Bruk Newton-Leibniz-formelen, beregne det bestemte integralet: 1. (2 + 2) 2. / 3. (4.) 5. 6. 7. 8. Efimov-Pospelov 7.324-7.352, 7.380-7.385,

Forelesning 7 Uekte integraler Uekte integraler er bestemte integraler der minst en av betingelsene for eksistensen av en bestemt (egentlig) integral ikke er oppfylt:) eller

14. leksjon. Trippelintegraler Mat. analyse, appl. matematikk, 3. semester Revisjon A1 I neste integral, gå til polare koordinater og ordne grensene for integrasjon i begge rekkefølgen:

Utdanningsdepartementet i den russiske føderasjonen Yaroslavl State University oppkalt etter. P.G. Demidova Institutt for diskret analyse FLY OG LINJE I ROM-problemer Yaroslavl Satt sammen av Ph.D.

MOSCOW AUTOMOBILE AND ROAD STATE TECHNICAL UNIVERSITY (MADI) INTEGRAL CALculUS Varianter av testoppgaver Oppgavebok MOSKVA AUTOMOBILE AND ROAD STATE TECHNICAL UNIVERSITY

Federal Agency for Railway Transport Ural State Transport University Institutt for høyere og anvendt matematikk P I Gnilomedov ANVENDELSER AV MULTIPLE OG KURVILINEÆRE INTEGRALER

UDDANNELSES- OG VITENSKAPSMINISTERIET I DEN RUSSISKE FØDERASJON FORBUNDSSTATEN AUTONOM UTDANNINGSINSTITUTION FOR HØYERE UDDANNELSE "SAMARA STATE AEROSPACE UNIVERSITY oppkalt etter

Vedlegg 5 Landbruksdepartementet i Den russiske føderasjonen Federal State Budgetary Education Institute of Higher Education "Saratov State Agrarian University"

ELEMENTER AV ANALYTISK GEOMETRI PÅ FLYET. Rett linje 1. Beregn omkretsen til en trekant hvis toppunkter er punktene A(6; 7), B(3; 3), C(1; 5). 2. Finn et punkt like langt fra punktene A(7;

Utdannings- og vitenskapsdepartementet i den russiske føderasjonen Yaroslavl State University oppkalt etter. P. G. Demidova Institutt for algebra og matematisk logikk Andre ordenskurver Del I Metodiske instruksjoner

Innhold Multiple integraler Konsept med multiple integraler Doble integraler. Regioner på planet................. Gjentatt integral................ 3.3 Beregning av dobbeltintegralet i kartesiske koordinater.. ...............

Praktisk leksjon 14 Emne: Parabelplan 1. Definisjon og kanonisk ligning av en parabel Geometriske egenskaper til en parabel. Den relative plasseringen av en parabel og en linje som går gjennom midten. Grunnleggende

1 De enkleste problemene med analytisk geometri på et plan 11 Avstand mellom to punkter Betrakt et rektangulært koordinatsystem (kartesisk, Fig. 1 Ethvert punkt M tilsvarer koordinatene OA x

TRANSPORTDEPARTEMENTET FOR DEN RUSSISKE FØDERASJONEN FEDERAL STATE EDUCATIONAL INSTITUTION OF HIGHER PROFESSIONAL EDUCATION ULYANOVSK HØYERE AVIATION SKOLE FOR CIVIL AVIATION (INSTITUTT)

Kapittel 5. Trippelintegral. 5.1. Definisjon av trippelintegral. Etter å ha introdusert begrepet dobbelt integral i forrige kapittel, vil det være naturlig å utføre dets videre generalisering til tredimensjonalt rom

ALGEBRAISKE LINJER PÅ PLANET.. LINJER I FØRSTE ORDEN (LINJER PÅ FLYET... GRUNNLEGGENDE TYPER AV LIGNINGER AV LINJER PÅ PLANET. En vektor som ikke er null n vinkelrett på en gitt linje kalles normal

UDDANNELSES- OG VITENSKAPSMINISTERIET I DEN RUSSISKE FØDERASJON RUSSISK STATSUVERSITET FOR OLJE OG GASS OPPNETT ETTER IMGUBKIN TS Filippova ANFILIPOV METODOLOGISKE INSTRUKSJONER for å studere emnet "Multiple and curvilinear

Penza State Pedagogical University oppkalt etter VGBelinsky OGNikitin FUNKSJONER AV FLERE VARIABLER INTEGRAL BEREGNING Lærebok Penza Utgitt etter beslutning fra redaksjonen og publiseringsavdelingen

Emne ELEMENTER AV ANALYTISK GEOMETRI PÅ FLYET OG I ROMMET Forelesning.. Rette linjer på planet Plan. Metode for koordinater på et plan.. Rett linje i kartesiske koordinater.. Betingelse for parallellitet og perpendikularitet

Moscow State Technical University oppkalt etter N.E. Bauman Fakultet for grunnleggende vitenskap Institutt for matematisk modellering A.N. Kaviakovykov, A.P. Kremenko

Kapittel 5 Overflateintegraler av typen (forts.) 5 Klasseoppgaver Oppgave 5 (4349) Regn ut integralet der en del av overflaten til kjeglen z d, x = ρ cos ϕ sin α, y = ρ sin ϕ sin α, z = ρ cos α (( ρh,

Federal Agency for Education Ural State Forestry University Institutt for styrke av materialer og teoretisk mekanikk V. A. Kalentyev V. M. Kalinin L. T. Raevskaya N. I. Chashchin

ELEMENTER AV ANALYTISK GEOMETRI KLASSIFISERING AV ET FLAN I TRE-DIMENSJONELT ROM Skriv en vektorligning av et plan og forklar betydningen av mengdene inkludert i denne ligningen Skriv en generell likning av et plan

3 Eksempel Skriv uttrykk for statiske momenter i et flatt materialeområde (D) Basert på formler (3) som tar hensyn til figuren (Φ), har vi: ρ, dd, ρ, dd Basert på den mekaniske betydningen av det statiske momentet,

Oppgave 1 Finn koordinatene til tyngdepunktet til halvsirkelen y = r 2 x 2. Oppgave 5 arealet til en del av overflaten z = 1 4 xy plassert inne i overflaten x 2 + y 2 = 16. Oppgave 2 Endre rekkefølgen på integreringen

UDDANNELSES- OG VITENSKAPSMINISTERIET I UKRAINE NATIONAL METALLURGICAL ACADEMY OF UKRAINE METODOLOGISKE INSTRUKSJONER for å løse problemer i faget høyere matematikk og praktiske testalternativer

Praktiske timer i løpet av høyere matematikk (III semester) basert på læreboken «Samling av individuelle oppgaver i høyere matematikk», bind 3, utg. Ryabushko A.P. for heltidsstudenter

Moscow State Technical University oppkalt etter N.E. Bauman Fakultet for grunnvitenskap Institutt for beregningsmatematikk og matematisk fysikk A.I. Levin FLERE INTEGRALER Elektronisk

Integralregning av en funksjon av flere variabler av en dobbel trippel krumlinjet langs buelengden (første type) overflate med hensyn til overflatearealet (første type) La funksjonen f() defineres

1.3. Leksjon 3 1.3.1. Beregning av trippelintegraler i kartesiske koordinater La være et romlig domene, D sin projeksjon på oksyplanet. Et område kalles -regular hvis noen vertikal linje

UNDERVISNINGSMINISTERIET I REPUBLIKKEN HVITERUSSLAND Hviterussisk nasjonale tekniske universitet Institutt for ingeniørmatematikk HØYERE MATEMATIKK Veiledning for å løse problemer for studenter innen mekanisk og teknologisk ingeniørfag

Praktisk leksjon 1 Emne: Hyperbelplan 1 Definisjon og kanonisk ligning av en hyperbel Geometriske egenskaper til en hyperbel Relativ posisjon til en hyperbel og en linje som går gjennom dens sentrum Asymptoter

Def . la,
,

.

Et sett kalles et lukket intervall eller en lukket bar i .

Settet kalles et åpent intervall

eller en åpen bjelke inn .

Def . Mål på intervaller Og mengden kalles:

(Mer presist
).

Def . Hvis
slik at
deretter intervallet kalles degenerert og
.

Egenskaper til gapmålet:

EN). Positivitet:
, og
da og bare når – degenerert.

b). Positiv homogenitet: .

V). Additivitet:

* For
slik at
;

* For
Og

.

G). Monotonicitet av tiltaket: .

Def . Diameteren på bjelken (gapet) er verdien:

Noter det
Og
– Dette er ikke det samme. For eksempel hvis – degenerert, altså
,en
(generelt sett).

Hvori: * ;

* ;*
.

Def . Totalitet
delspenn av intervallet kalt intervallpartisjon , Hvis: *;

*
; *
; *
; *
.

Omfanget
kalt partisjonsparameteren P(hvori
).

Def . Splitting kalt partisjonsforbedring , hvis alle elementene i partisjonen oppnådd ved å partisjonere partisjonselementene .

Indikert av:
. Leser: mindre eller større .

For forholdet "større - mindre" gjelder følgende:

*. transitivitet – ; *.
;

*.

; *.

|
.

§. Definisjon av multippelintegral

La
– tømmer (gap) inn ,
– oppdeling av gapet Jeg. Ved hvert intervall av partisjonen marker poenget
.

Vi får
skillevegg med markerte punkter for
.

Omfanget
kalles Riemann-integralsummen for funksjonen f (x) på intervallet Jeg ved skillevegg med markerte punkter
.

Def :
=
=
.

Utpeker – mange funksjoner integrert på bjelken Jeg la oss skrive:

Def : ε > 0 δ>0<.

Hvis for funksjonen f(x) på Jeg og skillevegger
- angi med
– den største og minste verdien av funksjonen f(x) på Jeg k deretter verdiene
=
Og
=
kalles nedre og øvre Darboux-summer.

§. Darboux-kriterium for eksistensen av en multippel integral.

T 0 . Å fungere
var integrert på bjelken (de.
) er nødvendig og tilstrekkelig slik at

. Δ▲.

Integrasjonen av en funksjon over en stråle i det euklidiske rom er definert. Hvordan kan man integrere en funksjon over et vilkårlig avgrenset sett fra det euklidiske rom?

La oss definere integralet til funksjonen f av mange
.

Def : La
Og
– begrenset, dvs.
. Funksjon
kaller vi den karakteristiske funksjonen til settet M.

Deretter:
≡
.

Definisjonen av et sett integral avhenger ikke av hvilken bjelke som inneholder M valgt, dvs.

.

Dette betyr at definisjonen av integralet over et sett er riktig.

En nødvendig betingelse for integrerbarhet.Å fungere f(x) på M være integrerbar er det nødvendig at f(x) var begrenset til M. Δ▲.

§. Egenskaper til flere integraler.

1  . Linearitet: Mange R M funksjoner som kan integreres på et sett M – lineær

plass, og
– lineær funksjonell.

2  . Normaliseringstilstand:
. En annen form for oppføring
bestemmer i hovedsak målet til et vilkårlig sett fra det euklidiske rom.

3  . Hvis det eksisterer et integral over et sett med Lebesgue-mål null, så er det

lik null.

Merk: En haug med M kalles settet med Lebesgue-mål null,

Hvis

slik at
Og
.

4  . EN.;b.;

V. Hvis
Og – atskilt fra null med M, Det

5  .
Og f=g p.v. (nesten overalt) på M, Det
.

6  . Additivitet: Hvis
Og
At

Generelt:
.

Δ. Det følger av likestillingen: ▲

7  . Monotone:
Og
At
.

8  . Integrering av ulikheter: hvis
ito

9  . La

. For å
, er det nødvendig og tilstrekkelig at det er et indre punkt i settet M, hvori f (x) > 0 og kontinuerlig.

10  . Integrerbarhet av den integrerbare funksjonsmodulen:
.

11  . Middelverditeorem:
,
på M bevarer skiltet og
, Det

Hvis settet M– sammenhengende og f(x) – kontinuerlig på
At
slik at
.

12  . For at integralet til en ikke-negativ funksjon skal være lik 0

nødvendig og tilstrekkelig til f(x) = 0 nesten overalt på M.

13  . Fubinis teorem. For dobbel integral:

La området
- rektangel:. Så, forutsatt at interne enkeltintegraler eksisterer, for å finne dobbeltintegralet, kan du fortsette til gjentatt integrasjon (se fig. a):

, eller

Hvis integrasjonsdomenet ikke er et rektangel, er Fubinis teorem fortsatt gyldig og har formen (se fig. b):

. (*)

Merk: De ytre grensene for integrasjon må være konstanter; de interne grensene for integrasjon kan avhenge av variabelen som integrasjonen ennå ikke skal utføres over.

Formel (*) kan oppnås ved å bruke den angitte karakteristiske funksjonen D.

For flere integraler:

La og noen delmengder av euklidiske rom Og . La oss definere det kartesiske produktet av disse settene, som er en delmengde av det euklidiske rommet
:.

Deretter Fubinis teorem for
har formen:
.

Teoremet gjelder også for bjelker X Og Y, og for mer komplekse konfigurasjoner.

Eksempler:

1 0 . Regne ut
, hvis grensen til området
gitt av ligningene:

. Når vi finner skjæringspunktene til kurvene som definerer grensen til området, får vi to punkter:

. Da gir et mulig arrangement av integrasjonsgrenser ved overgang til itererte integraler:

EN).
;

0 . Endre integrasjonsrekkefølgen i det itererte integralet:

–

Oppskrift: Når du setter integrasjonsgrenser i en dobbel integral, anbefales det å starte med de ytre integrasjonsgrensene.

0 . Regne ut:

, Hvis

Overgang til itererte integraler gir:
.

Samtidig, i et trippelintegral, må plassering av grenser begynne med de interne grensene for integrasjon. Deretter prosjekterer området V til flyet xOy

sette grenser i området D– ligger i et fly xOy.

4 0 . Endre integrasjonsrekkefølgen i det itererte integralet:
.

Multippel integral

integral av en funksjon spesifisert i et område på planet, i tre dimensjoner eller n-dimensjonalt rom. Blant K. og. skille mellom doble integraler, trippelintegraler osv. n-flere integraler.

La funksjonen f(x, y) er gitt i et eller annet område D flyet xOy. La oss dele opp området D på n delområder d jeg, hvis områder er like er jeg, velge i hvert område d i punkt ( ξi, ηi) (cm. ris. ) og komponer integralsummen

Hvis, med en ubegrenset reduksjon i den maksimale diameteren på delarealer d i beløp S ha en grense uavhengig av valg av poeng ( ξi, ηi), så kalles denne grensen det doble integralet til funksjonen f(x, y) etter region D og betegne

Trippelintegralet er definert på samme måte, og generelt sett, n-flere integral.

For eksistensen av en dobbel integral er det tilstrekkelig, for eksempel at regionen D var en lukket kvadratisk region (Se kvadratbar region), og funksjonen f(x, y) var kontinuerlig i D. K. og. har en rekke egenskaper som ligner egenskapene til enkle integraler . For å beregne K. og. vanligvis føre det til en iterert integral (Se Iterated integral). I spesielle tilfeller for K.s opplysninger og. Greens formel og Ostrogradskys formel kan tjene som integraler av lavere dimensjon. K. og. har omfattende bruksområder: de brukes til å uttrykke volumene til legemer, deres masse, statiske momenter, treghetsmomenter, etc.

Stor sovjetisk leksikon. - M.: Sovjetisk leksikon. 1969-1978 .

Se hva "Multiple integral" er i andre ordbøker:

Integral av en funksjon av flere variabler. Det bestemmes ved å bruke integralsummer, lik det bestemte integralet til en funksjon av en variabel (se Integralregning). Avhengig av antall variabler er det dobbel, trippel, n... ... Stor encyklopedisk ordbok

Bestemt integral av en funksjon av flere variabler. Det finnes ulike konsepter av K. og. (Riemann-integral, Lebesgue-integral, Lebesgue Stieltjes-integral, etc.). Multippel Riemann-integralet introduseres på grunnlag av Jordan-målet. La E være Jordan-målbar... ... Matematisk leksikon

I matematisk analyse er et multippel- eller multippelintegral et sett med integraler hentet fra variabler. For eksempel: Merk: et multippelintegral er et bestemt integral; beregningen resulterer alltid i et tall. Innhold 1... ...Wikipedia

Integral av en funksjon av flere variabler. Bestemmes ved bruk av integralsummer, tilsvarende definert. integral av en funksjon av én variabel (se integralregning). Avhengig av antall variabler er det dobbel, trippel, i... ... Naturvitenskap. encyklopedisk ordbok

Merk: overalt i denne artikkelen der tegnet brukes, menes (multippel) Riemann-integralet, med mindre annet er angitt; Overalt i denne artikkelen hvor vi snakker om målbarheten til et sett, mener vi jordansk målbarhet, hvis ikke... ... Wikipedia

Et multippelintegral av formen where, som er gjennomsnittsverdien av graden 2k av modulen til en trigonometrisk sum. Vinogradovs teorem om verdien av dette integralet, middelverditeoremet, ligger til grunn for estimater av Weyl-summer. Litteratur Vinogradova inte... Wikipedia

Bestemt integral som arealet til en figur Dette begrepet har andre betydninger, se Integral (betydninger). Integral av en funksjon ... Wikipedia

Et integral der integrasjon over forskjellige variabler utføres sekvensielt, dvs. et integral av formen (1) Funksjonen f(x, y) er definert på mengden A som ligger i det direkte produktet XX Y av mellomrommene X og Y, der s er gitt endelige mål mx og my, … … Matematisk leksikon

En integral tatt langs en hvilken som helst kurve på et plan eller i rommet. Det er K. og. 1. og 2. type. K. og. Type 1 oppstår for eksempel når man vurderer problemet med å beregne massen til en kurve med variabel tetthet; det er utpekt ...... Stor sovjetisk leksikon

La oss dvele i noen detalj ved Ostrogradskys arbeid med flere integraler.

Ostrogradskys formel for å transformere en trippelintegral til en dobbel, som vi vanligvis skriver i formen

der div A er divergensen til feltet til vektor A,

Аn er skalarproduktet av vektor A og enhetsvektoren til den ytre normalen n av grenseoverflaten; i den matematiske litteraturen var det ofte tidligere assosiert med navnene Gauss og Green.

Faktisk, i Gauss sitt arbeid om tiltrekning av sfæroider, kan man bare se helt spesielle tilfeller av formel (1), for eksempel med P=x, Q=R=0 osv. Når det gjelder J. Green, i hans arbeid på teorien om elektrisitet og det er ingen magnetisme i det hele tatt i formel (1); den utleder et annet forhold mellom trippel- og dobbelintegraler, nemlig Greens formel for Laplace-operatoren, som kan skrives i formen

Selvfølgelig kan vi utlede formel (1) fra (2), forutsatt

og på samme måte er det mulig å få formel (2) fra formel (1), men Green tenkte ikke på å gjøre dette.

hvor til venstre er integralet over volumet, og til høyre er integralet over grenseflaten, og disse er retningscosinusene til den ytre normalen.

Ostrogradskys Paris-manuskripter vitner med full sikkerhet om at både oppdagelsen og det første budskapet til integralsetningen (1) tilhører ham. Det ble først uttalt og bevist, nøyaktig slik de nå gjør, i "Proof of a Theorem of the Integral Calculus", presentert for Paris Academy of Sciences 13. februar 1826, hvoretter det ble formulert igjen i den delen av "Memoir on the Diffusion of Heat in Solids." ", som Ostrogradsky presenterte den 6. august 1827. "Memoir" ble gitt for anmeldelse til Fourier og Poisson, og sistnevnte leste den absolutt, som det fremgår av oppføringen på den første sider i begge deler av manuskriptet. Ideen om å tilskrive seg selv teoremet, som han ble kjent med i arbeidet til Ostrogradsky to år før han presenterte sitt arbeid med teorien om elastisitet, falt ikke en gang opp for Poisson.

Når det gjelder forholdet mellom verkene på flere integraler av Ostrogradsky og Green, husker vi at i "Note on the Theory of Heat" ble det utledet en formel som omfavner Greens egen formel som et veldig spesielt tilfelle. Den nå uvanlige Cauchy-symbolikken som ble brukt av Ostrogradsky i "notatet" inntil nylig skjulte denne viktige oppdagelsen for forskere. Greene beholder selvfølgelig æren av oppdagelsen og den første publiseringen i 1828 av formelen for Laplace-operatører som bærer navnet hans.

Oppdagelsen av en formel for å transformere et trippelintegral til et dobbeltintegral hjalp Ostrogradsky med å løse problemet med å variere et n-fold integral, nemlig å utlede den generelle formelen for å transformere integralet fra et uttrykk for typen divergens over en n- dimensjonalt domene og integralet over overflaten S som avgrenser det med ligningen L(x,y, z,...)=0. Hvis vi holder oss til den forrige notasjonen, har formelen formen

Ostrogradsky brukte imidlertid ikke de geometriske bildene og begrepene vi bruker: geometrien til flerdimensjonale rom eksisterte ennå ikke på den tiden.

I "Memoir on the Calculus of Variations of Multiple Integrals" vurderes to viktigere spørsmål i teorien om slike integraler. Først utleder Ostrogradsky en formel for å endre variabler i et flerdimensjonalt integral; for det andre gir han for første gang en fullstendig og nøyaktig beskrivelse av metoden for å beregne et n-fold integral ved å bruke n suksessive integrasjoner over hver av variablene innenfor de passende grensene. Til slutt, fra formlene i dette memoaret, er den generelle regelen for differensiering med hensyn til parameteren til et flerdimensjonalt integral lett avledet, når ikke bare integrandfunksjonen, men også grensen til integrasjonsdomenet avhenger av denne parameteren. Den navngitte regelen følger av formlene i memoarene på en så naturlig måte at senere matematikere til og med identifiserte den med en av formlene i denne memoarboken.

Ostrogradsky viet et spesielt arbeid til å endre variabler i flere integraler. For dobbeltintegralet utledet Euler den tilsvarende regelen ved å bruke formelle transformasjoner; for trippelintegralet avledet Lagrange den. Men selv om Lagranges resultat er riktig, var resonnementet hans ikke nøyaktig: han så ut til å gå ut fra det faktum at volumene i de gamle og nye variablene - koordinater - er like med hverandre. Ostrogradsky gjorde en lignende feil i begynnelsen i den nettopp nevnte utledningen av regelen for å erstatte variabler. I artikkelen «On the Transformation of Variables in Multiple Integrals» avslørte Ostrogradsky Lagranges feil, og skisserte også for første gang den visuelle geometriske metoden for å transformere variabler i en dobbel integral, som, i en litt mer streng form, også presenteres i våre manualer. Når man erstatter variabler i integralet ved hjelp av formler, deles nemlig integrasjonsdomenet av koordinatlinjene til to systemer u=const, v=const i uendelig små krumlinjede firkanter. Deretter kan integralet oppnås ved først å legge sammen de av elementene som tilsvarer en uendelig smal buet stripe, og deretter fortsette å summere elementene i striper til de alle er oppbrukt. En enkel utregning gir for arealet, som opp til små høyere ordens, kan betraktes som et parallellogram, er uttrykket hvor, valgt slik at arealet er positivt. Resultatet er den velkjente formelen

For en funksjon av to variabler spesifisert som z = f(x, y) .

Dobbeltintegralet er skrevet som følger:

Her D– en flat figur avgrenset av linjer, hvis uttrykk (likheter) er gitt i oppgaven med å beregne dobbeltintegralet. Venstre og høyre er likheter der variabelen til venstre er x, og over og under – etter likheter der variabelen til venstre er y. Dette stedet fortsetter å være en av de viktigste for å forstå teknikken for å beregne dobbeltintegralet.

Beregn dobbeltintegral - betyr å finne et tall som er lik arealet til den nevnte figuren D .

Helt til vi berører doble integraldefinisjoner , og vi skal lære å beregne det. Det er lettere å forstå hva et dobbeltintegral er når du har løst flere oppgaver for å regne det ut, så du finner definisjonen av et dobbeltintegral på slutten av denne leksjonen. Ser vi litt fremover, kan vi bare merke oss at definisjonen av et dobbeltintegral også er relatert til den nevnte figuren D .

Hvis figuren D er et rektangel, alle linjene som begrenser det er rette linjer. Hvis figuren D- er krumlinjet, så er den til venstre og høyre begrenset av rette linjer, og over og under av buede linjer, gitt av likhetene som er gitt i oppgaven. Det er også tilfeller når en figur D- en trekant, men mer om slike saker litt lenger.

For å beregne dobbeltintegralet er det derfor nødvendig å sortere linjene som grenser til figuren D, som har et strengt navn - regionen for integrering. Sorter i venstre og høyre og topp og bunn. Dette vil være nødvendig når redusere en dobbel integral til en iterert integral – metode for å beregne dobbeltintegralet.

Tilfelle av et rektangulært område:

Tilfelle av et buet område:

Og dette er allerede en løsning på de kjente bestemte integralene, der de øvre og nedre grensene for integrasjon er gitt. Uttrykk som definerer linjer som avgrenser en figur D, vil være grensene for integrasjon for de vanlige bestemte integralene, som vi allerede nærmer oss.

Redusere en dobbel integral til en gjentatt

Tilfelle av en rektangulær region

La det være en dobbel integral for en slik funksjon

Til evaluer dette doble integralet , må vi redusere det til et iterert integral, som har formen

Først må du beregne det indre (høyre) bestemte integralet, deretter det ytre (venstre) bestemte integralet.

Du kan bytte roller x Og y

Eksempel 1. Beregn dobbeltintegral

Vi beregner det indre (høyre) integralet, og betrakter y som en konstant. Vi forstår det.

Eksempel 2. Beregn dobbeltintegral

Løsning. Vi reduserer dette doble integralet til et iterert integral

På tegningen konstruerer vi integrasjonsregionen:

Nå beregner vi det ytre (venstre) integralet av det nettopp beregnede indre (høyre):

Resultatet vil være løsningen på dette doble integralet.

Regn ut dobbeltintegralet selv og se deretter på løsningen

Tilfellet av et buet eller trekantet område

La oss igjen få en funksjon av to variabler f(x, y) , og begrensningene for D: allerede av en litt annen type:

Denne oppføringen betyr at figuren D venstre og høyre er begrenset, som i tilfelle av en rettlinjet region - rette linjer x = en Og x = b, men under og over er kurver som er gitt av ligningene og . Med andre ord, og er funksjoner.

La en slik funksjon også ha et dobbelt integral

For å evaluere dette doble integralet, må vi redusere det til et iterert integral, som har formen

Her er grensene for integrering en Og b- tall, og og - funksjoner. Når det gjelder et trekantet område, er en av funksjonene eller ligningen til en rett linje. Denne saken vil bli diskutert i eksempel 3.

Som i tilfellet med et rettlinjet område, må du først beregne det høyre bestemte integralet, deretter det venstre bestemte integralet.

På samme måte kan du bytte roller x Og y. Da vil det gjentatte integralet ha formen

Et slikt gjentatt integral må løses på nøyaktig samme måte: først - det indre (høyre) integralet, deretter - det ytre (venstre).

Eksempel 5. Beregn dobbeltintegral

Løsning. Vi reduserer dette doble integralet til et iterert integral

På tegningen konstruerer vi integrasjonsregionen og ser at den er trekantet:

Vi beregner det indre (høyre) integralet, og betrakter x som en konstant. Vi forstår det.

Nå beregner vi det ytre (venstre) integralet av det nettopp beregnede indre (høyre). Først presenterer vi dette integralet som en sum av integraler:

Vi beregner det første leddet:

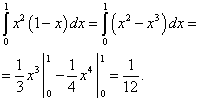
Vi beregner det andre leddet:

Vi beregner det tredje leddet:

Vi får summen, som vil være løsningen på dette doble integralet:

Eksempel 6. Beregn dobbeltintegral

Løsning. Vi reduserer dette doble integralet til et iterert integral

På tegningen konstruerer vi integrasjonsregionen:

Vi beregner det indre (høyre) integralet, og betrakter x som en konstant. Vi forstår det.

Nå beregner vi det ytre (venstre) integralet av det nettopp beregnede indre (høyre):

Resultatet vil være løsningen på dette doble integralet.

x-rett og galt y-riktige og uriktige integreringsdomener

Det hender at domenet for integrering av et dobbeltintegral er begrenset av slike linjer at det blir nødvendig å dele integrasjonsdomenet i deler og løse hver tilsvarende gjentatte integral separat. Dette er tilfeller når:

1) integrasjonsområdet er en figur som har to eller flere rette eller buede linjer i form av en nedre eller øvre (venstre eller høyre) grense;

2) integrasjonsområdet er en figur hvis grense linjene krysser på mer enn to punkter.

Hvis ovenstående gjelder venstre eller høyre grense av integrasjonsdomenet, det vil si begrensningene definert av linjene uttrykt i form av x, da kalles integrasjonsdomenet x-feil. Hvis linjen y = y0 skjærer den tilsvarende grensen på bare ett punkt, og hvis grensen bare er en rett linje eller kurve, kalles integrasjonsdomenet x-riktig

Tilsvarende, hvis grensen definert av linjer uttrykt gjennom y, rett x = x0 skjærer i mer enn ett punkt eller hvis grensen er mer enn én rett linje eller kurve, kalles integrasjonsdomenet y-feil. Vis nå skiltene y- Det riktige området er antagelig ganske enkelt.

Så langt har vi sett på eksempler med x-feil og y-riktige integreringsområder. Vurder nå tilfeller når korrekthetsbetingelsen er brutt.

Eksempel 7. Beregn et dobbeltintegral hvis integrasjonsdomene er begrenset av linjer y = x , xy = 1 , y = 2 .

Løsning. Domenet for integrering er y-feil, siden dens nedre grense ikke kan spesifiseres med en enkelt linje y = y(x) . Som det fremgår av figuren over, består den nedre grensen av y = x(mørk burgunder) og xy= 1 (grønn). Derfor direkte x= 1 (svart) kan vi dele integrasjonsdomenet i to deler - og .

Dette doble integralet beregnes som følger:

Endre rekkefølgen for integrering

Som nevnt ovenfor, etter å ha redusert dobbeltintegralet til et iterert integral, kan du endre variablene x Og y roller, eller med andre ord endre rekkefølgen på integreringen.

Endringen i integrasjonsrekkefølgen kan billedlig beskrives med følgende ord fra O'Henry: "Dette er hvordan en jungelbeboer - et dyr - oppfører seg når han kommer inn i et bur, og dette er hvordan en innbygger i bur - en mann - oppfører seg når han går seg vill i tvilens jungel." Resultatet, ifølge O'Henry, er det samme og det samme: "Chalmers rev brevet i tusen bittesmå strimler og begynte å rive i det dyre teppet hans mens han gikk tilbake og videre på det." ( O.Henry. Scheherazade fra Madison Square.)

Deretter, hvis vår venstre integral over variabelen x, og den rette - av y, så etter å ha endret rekkefølgen på integreringen vil alt være omvendt. Da må grensene for integrasjon for det "nye" spillet "lånes" fra den "gamle" X, og grensene for integrasjon for den "nye" X må hentes i skjemaet invers funksjon, løse for x ligningen som satte grensen for y.

Eksempel 8.

Løsning. Etter å ha endret rekkefølgen på integreringen, vil integralet over y bli venstrehendt, og integralet over x blir høyrehendt. Vi vil låne grensene for integrasjon for det "nye" spillet fra den "gamle" X, det vil si at den nedre grensen er lik null, og den øvre grensen er lik en. Grensene for integrasjon for det "gamle" spillet er gitt av ligningene og . Etter å ha løst disse ligningene for x, får vi nye grenser for integrasjon for x:

(nedre) og (øvre).

Etter å ha endret integrasjonsrekkefølgen, vil det gjentatte integralet bli skrevet som følger:

Etter å ha endret rekkefølgen av integrering i en dobbel integral, blir integrasjonsdomenet ofte til y-feil eller x-feil (se forrige avsnitt). Deretter må du dele integrasjonsdomenet i deler og løse hver tilsvarende itererte integral separat.

Siden det å dele opp integreringsdomenet i deler byr på visse vanskeligheter for mange elever, vil vi ikke begrense oss til eksemplet gitt i forrige avsnitt, men se på et par flere eksempler.

Eksempel 9. Endre integrasjonsrekkefølge for iterert integral

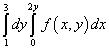Løsning. Så, området for integrering av dette itererte integralet er begrenset av rette linjer y = 1 , y = 3 , x = 0 , x = 2y .

Ved integrering i en annen rekkefølge, består den nedre grensen av regionen av to rette linjer: AB Og B.C., som er gitt av ligningene y= 1 og y = x/2, som kan sees i figuren nedenfor.

Veien ut av slik usikkerhet er å dele integrasjonsdomenet i to deler. Inndelingen av integrasjonsdomenet vil være en rett linje BM. Vi beregner nye grenser for integrasjon ved å finne den inverse funksjonen. I henhold til denne løsningen vil det gjentatte integralet etter endring av integrasjonsrekkefølgen være lik summen av to integraler:

Naturligvis vil det samme være løsningen på dobbeltintegralet, som reduseres til det gjentatte integralet gitt i tilstanden til dette eksemplet.

Eksempel 10. Endre integrasjonsrekkefølge for iterert integral

Løsning. Så domenet for integrering av det itererte integralet er begrenset til rette linjer x = 0 , x= 2 og kurver og .

Som du kan se i figuren under, en rett linje parallelt med aksen 0x, vil krysse den nedre grensen til integrasjonsdomenet på mer enn to punkter.

Derfor deler vi integrasjonsdomenet i tre deler ved rette linjer, som er tegnet i svart i figuren. Vi beregner nye grenser for integrasjon ved å finne den inverse funksjonen. Grensene for de tre nye integreringsområdene vil være som følger.

I henhold til denne løsningen vil det gjentatte integralet etter endring av integrasjonsrekkefølgen være lik summen av tre integraler:

Den samme summen av tre integraler vil være lik dobbeltintegralet, som reduseres til det gjentatte integralet gitt i tilstanden til dette eksemplet.

Og likevel forstyrrer force majeure-omstendigheter ofte studentene allerede på forrige trinn - setter grensene for integrering. Angst og forvirring er ikke uten noe grunnlag: hvis for å dele integrasjonsregionen i deler er det vanligvis nok å se nøye på tegningen og løse den gjentatte integralen - tabellen over integraler, så er det nødvendig med litt treningserfaring for å sette grensene av integrasjon. La oss gå gjennom et eksempel der vi kun vil fokusere på å sette grensene for integrasjon og - nesten automatisk - på å partisjonere regionen og utelate selve løsningen.

Eksempel 11. Finn grensene for integrasjon av en dobbel integral hvis domenet for integrasjon D gitt som følger:

y - 2x ≤ 0;
2 år - x ≥ 0;
xy ≤ 2.

Løsning. Eksplisitt (via x Og y"uten urenheter") linjene som begrenser integrasjonsregionen er ikke spesifisert. Siden de for X oftest viser seg å være rette linjer som på ett punkt berører de øvre og nedre grensene, uttrykt gjennom i-en, vil vi gå nøyaktig langs denne banen. Ved endring av integreringsrekkefølgen får vi dessuten en integreringsregion med samme areal. La oss løse ulikhetene for spillet og få:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

Vi bygger de resulterende linjene på tegningen. Grensene for integrasjon over x er faktisk linjene x= 0 og x= 2 . Men området for integrering viste seg å være y-feil, siden dens øvre grense ikke kan spesifiseres med en enkelt linje y = y(x) .